梯度提升树 | Gradient Boosting Decision Tree (GBDT)
GBDT 有很多简称,有 GBT(Gradient Boosting Tree), GTB(Gradient Tree Boosting ), GBRT(Gradient Boosting Regression Tree), MART(Multiple Additive Regression Tree)
一、GBDT回归原理
1.1、残差更新:
举个简单的例子: 预测一个同学本次的考试成绩, 根据他之前的考试成绩的平均值来预测本次结果, 在训练算法时, 将预测值(之前分数的平均分) 分数和实际的分数相减, 得到的值就是残差;(在梯度提升回归树中, 残差值越小越好)
之后按照梯度下降的思想不断更新残差:
residual 是上一轮的残差, learning_rate是残差更新的系数, 也就是学习率,在定义算法时定义的参数
直到循环的次数达到事先预设好的次数就结束, 预设次数是参数n_estimators决定的(默认是100)
示例: 现有一组数据, X代表消费金额和上网时长, 通过X预测任务的年龄.
import numpy as np from sklearn.ensemble import GradientBoostingRegressor import matplotlib.pyplot as plt from sklearn import tree X = np.array([[600,0.8],[800,1.2],[1500,10],[2500,3]]) y = np.array([14,16,24,26]) # loss = ls 最小二乘法 learning_rate = 0.1 # 残差更新系数 gbdt = GradientBoostingRegressor(n_estimators=1,loss = 'ls', learning_rate=0.1) # learning_rate 学习率 gbdt.fit(X,y_true) #训练 y_ = gbdt.predict(X) #预测 # 用代码实现残差更新 residual = y - y.mean() # 残差(第一棵树); 预测的初始值给训练数据的平均值 print(residual) ''' array([-6., -4., 4., 6.]) ''' result = y - residual # 第一棵树的预测值 residual = residual - learning_rate*residual # 对残差进行更新(残差值越小越好) - 第二棵树的残差 result = y - residual # 第二棵树的预测值 ''' array([-3., -2., 2., 3.]) ''' # 以此类推, 残差值会越来越小, 预测的结果也就月接近真实值 # 算法模型实现残差更新 gbdt[0, 0].predict(X) # 得到残差 gbdt.predict(X) # 预测值
1.2、分裂标准
知识扩展:
均方误差: 预测值和真实值的差的平方的平均值
MSE的值越小,说明预测模型描述实验数据具有更好的精确度
均方根误差: 均方误差开方
平均绝对误差: 预测值和真实值的绝对值求和的平方的平均值
平均绝对误差能更好地反映预测值误差的实际情况.
方差: 数组内每个数和该数组的平均值的差的平方的和的平均值
标准差(均方差): 方差开方
标准差能反映一个数据集的离散程度, 标准差越大,数据越离散
梯度提升回归树是使用了决策树的算法, 所以在预测的时候可以将过程可视化出来,方便更直观的观察整个过程;在这个过程中我们一般使用目标值的均方误差来作为分裂的标准:
同样是上面那个例子, 在第一次分裂的时候我们可以根据消费金额和上网时长来分裂, 这里以消费金额为例, 我们有决策树模型:
X.iloc[:, 0] = [600, 800,1500,2500] —> y = [14, 16,24,26]
- ①: [[600], [800,1500,2500]] —> [[14], [16,24,26]]
此时计算目标值均方误差(初次年龄预测值为测试数据的平均值):
再乘以各子数组在总数组中所占的比例:
同理可以算出另外两种决策树模型的均方误差:
- ②: [[600, 800], [1500,2500]] —> [[14,16], [24,26]]
均方误差为: 1
- ③: [[600, 800, 1500], [2500]] —> [[14,16,24], [26]]
均方误差为: 14
均方误差越小,说明该模型预测的结果和真实值越接近,所以,不选它还选谁?
以上的推导只是梯度提升回归树的第一棵树的第一次裂变, 我们可以设置相应的参数,规定树的裂变次数, 所以按照以上的原理方式依次进行裂变,即可的到最精确的回归模型
二、GBDT分类原理
2.1、信息熵和交叉熵:
信息熵:
交叉熵: (pk是真实分布比例, qk是非真实分布(预测分布比例))
2.2、GBDT原理概述
GBDT 是先有 GB(梯度提升),再有 DT(决策树),所以我们先从 GB 讲起.
boosting 就是通过训练多个弱分类器来组合成一个强分类器,形式如下:
其中, 是弱分类器,比如在 AdaBoost提升中是 C4.5决策树; 是最终得到的强分类器; 而本篇中的GBDT的弱分类器则是CART回归树(在GBDT中不管是回归问题还是分类问题,弱学习器都是决策回归树)
最深梯度下降法(Steepest Gradient Descent):
1、给定一个起点
2、更新 的位置:
其中: 表示在 处的导数
3、直到 足够小, 或者 足够小
以上迭代过程可以理解为: 整个寻优的过程就是小步快跑的过程,每跑一小步,都往函数当前下降最快的那个方向走一点,直到达到可接受的点
这个迭代过程展开得到寻优的结果:
所以我们可以将最深梯度下降法运用到boosting, 不同的是最深梯度下降法求得的是一个最优值, 此时我们是要求得一个最优的函数
2.3、二分类损失函数(交叉熵):
y是真实分布, p是非真实分布; 梯度提升回归森林是由决策回归树组成 , F(x)表示GBDT的学习器, 通过p这个sigmoid函数将其转换为相应的概率(多分类问题通过softmax函数转化概率)
带入p化简:(此处log默认以e为底)
对损失函数在Fm − 1(x) 处应用二级泰勒展开(方便计算γmj):
相当于梯度下降中的梯度(这里可以理解为弱学习器的拟合函数), 表示第m轮的第j个叶节点的预测值
是第m轮学习的第j个叶节点, 是上一轮学习的结果
接着对损失函数的泰勒展开式求导:
上面泰勒展开式中有损失函数的一阶导数和二阶导数,所以:
- 对损失函数求导(一阶导数):
2. 对损失函数求导(二阶导数):
此时令:
则损失函数的一阶导数为:
损失函数的二阶导数为:
令导数为0, 并将损失函数的一阶导数和二阶导数带进去, 求γmj的最优函数:
2.4、求初始值
此时为的最小值, 当的导数为零时取最小值, 也就是取得最小值,即为初始值
对H(ρ)求导
令H′(ρ) = 0 ,求ρ
2.5、最强学习器
根据:
其中:
而此时初始值:
γ的值为:
的值为模型参数,
经过足够多的学习次数, 最终能得出一个最优学习器
2.6、代码实现梯度提升分类树
代码实现和模型调用进行对比
2.6.1、模型调用(二分类结果)
import numpy as np from sklearn.ensemble import GradientBoostingClassifier from sklearn import tree # 构造数据 X = np.arange(1,11).reshape(-1,1) y = np.array([0,0,0,1,1]*2) # 定义算法 # 默认情况下,损失函数就是Log-loss == 交叉熵! clf = GradientBoostingClassifier(n_estimators=100,learning_rate=0.1,max_depth=1) clf.fit(X,y) y_ = clf.predict(X) print('真实的类别:',y) print('算法的预测:',y_) ''' 真实的类别: [0 0 0 1 1 0 0 0 1 1] 算法的预测: [0 0 0 1 1 0 0 0 1 1] ''' # 绘制决策树 # 第一棵树 _ = tree.plot_tree(clf[0,0],filled=True) # 第二棵树 _ = tree.plot_tree(clf[1,0],filled=True) # 第三棵树 _ = tree.plot_tree(clf[2,0],filled=True)
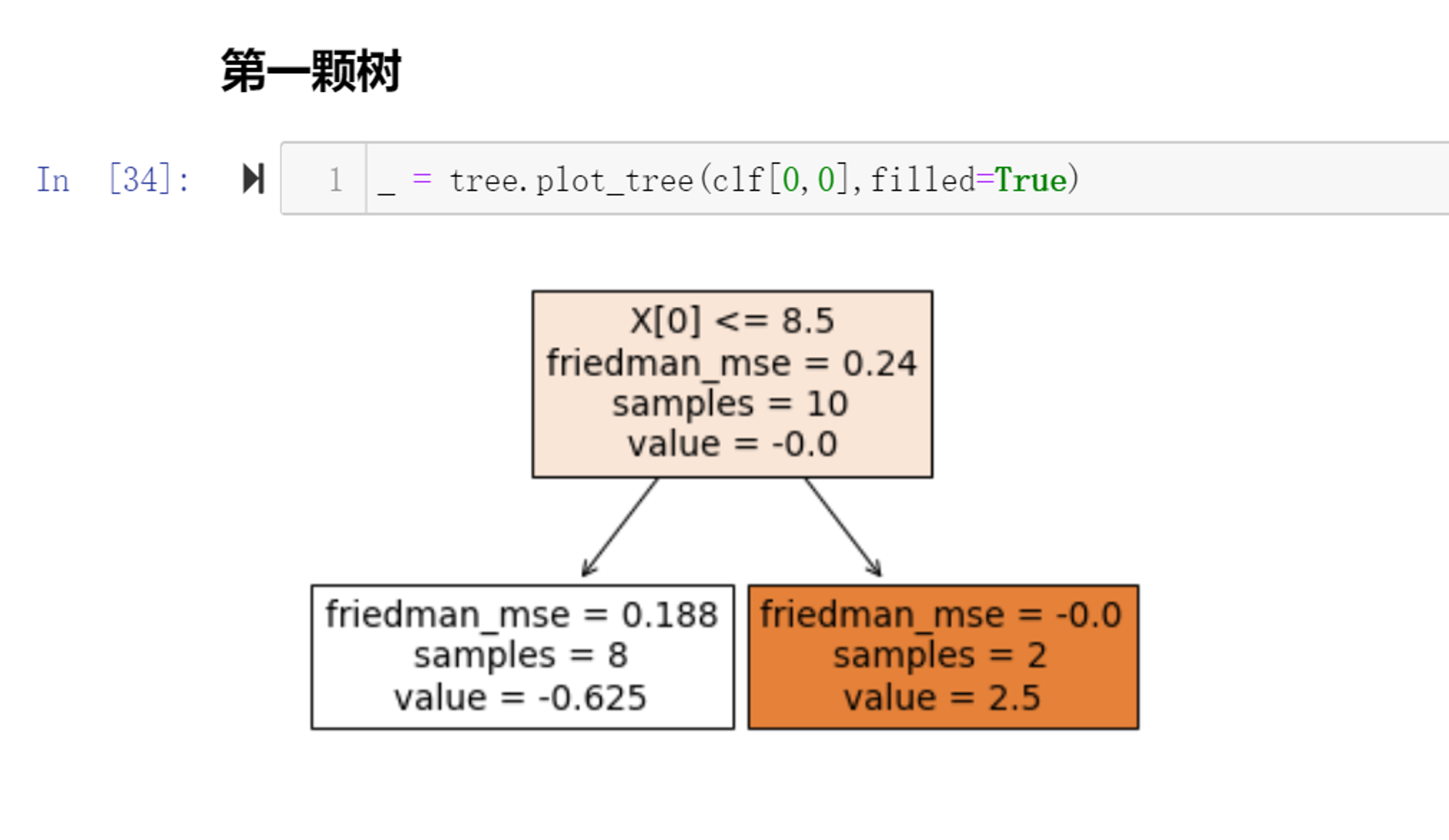
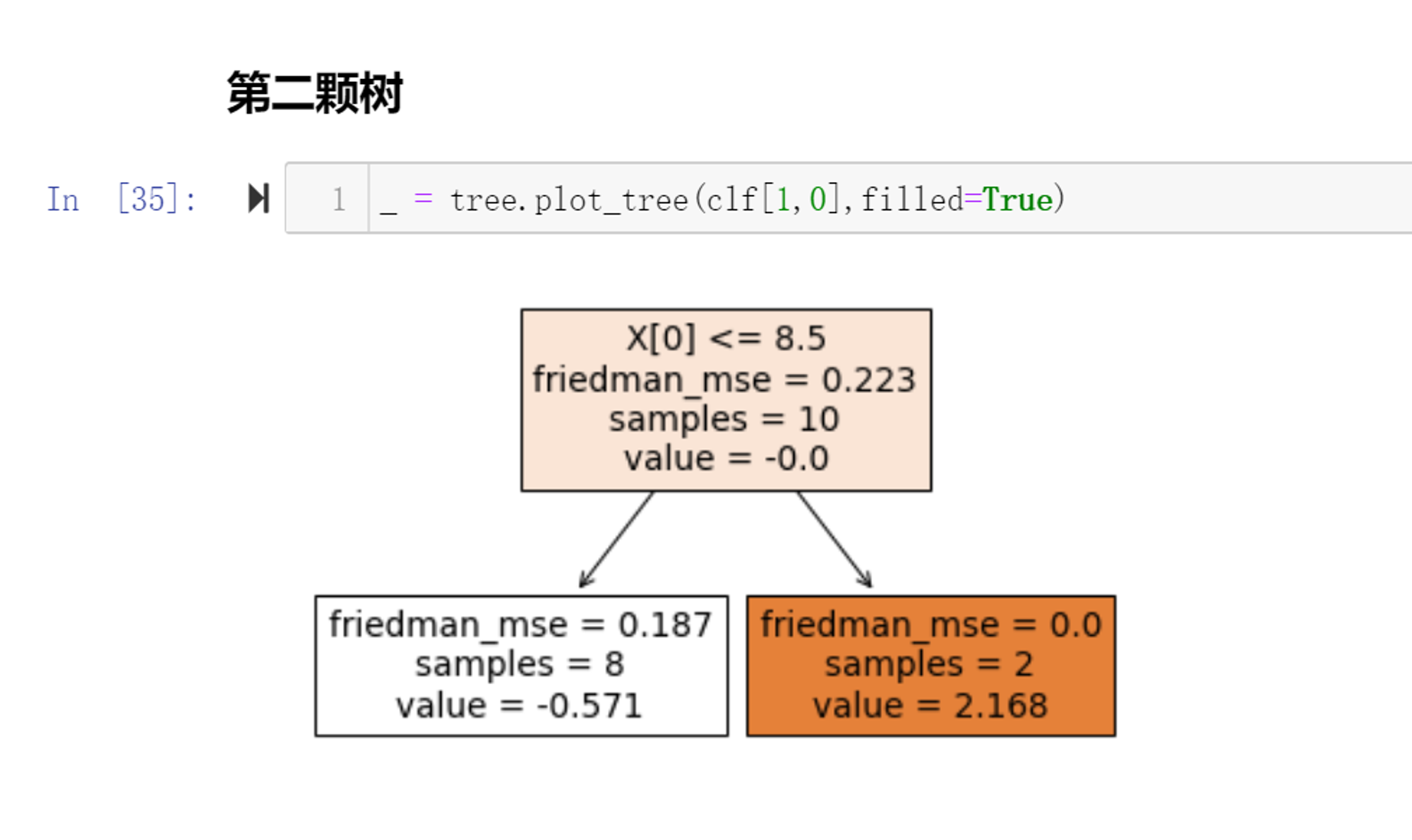

2.6.2、代码实现(二分类结果)
import numpy as np from sklearn.ensemble import GradientBoostingClassifier from sklearn import tree # 构造数据 X = np.arange(1,11).reshape(-1,1) y = np.array([0,0,0,1,1]*2)
计算初始值:
此处表示类别, 其值为1(1表示true)
# 二分类问题,类别 :0,1 # [0 0 0 1 1 0 0 0 1 1] F0 = np.log(4/6) ''' -0.40546510810816444 '''
计算ỹ 导数就是梯度,负梯度
# 函数F(X) 初始值F0的负梯度 yderivative0 = y - 1/(1 + np.exp(-F0)) ''' array([-0.4, -0.4, -0.4, 0.6, 0.6, -0.4, -0.4, -0.4, 0.6, 0.6]) '''
拟合第一棵树:
# 分裂标准 mse for i in range(1,11): if i ==10: mse = ((yderivative0 - yderivative0.mean())**2).mean() else: left_mse = ((yderivative0[:i] - yderivative0[:i].mean())**2).mean() right_mse = ((yderivative0[i:] - yderivative0[i:].mean())**2).mean() mse = left_mse*i/10 + right_mse*(10-i)/10 print('从第%d个进行切分'%(i),np.round(mse,4)) # 从第八个样本这里进行分类,最优的选择,和算法第一颗画图的结果一致 ''' 从第1个进行切分 0.2222 从第2个进行切分 0.2 从第3个进行切分 0.1714 从第4个进行切分 0.225 从第5个进行切分 0.24 从第6个进行切分 0.2333 从第7个进行切分 0.2095 从第8个进行切分 0.15 从第9个进行切分 0.2 从第10个进行切分 0.24 '''
计算左、右两侧叶子的预测值:
# 左边分支 gamma1 = np.round(yderivative0[:8].sum()/((y[:8] - yderivative0[:8])*(1 - y[:8] + yderivative0[:8])).sum(),3) print('左边决策树分支,预测值:',gamma1) ''' 左边决策树分支,预测值: -0.625 ''' # 右边分支 gamma2 =np.round(yderivative0[8:].sum()/((y[8:] - yderivative0[8:])*(1 - y[8:] + yderivative0[8:])).sum(),3) print('右边决策树分支,预测值:',gamma2) ''' 右边决策树分支,预测值: 2.5 '''
第一棵树拟合完毕, 代码实现的,和算法中的第一颗树(画图显示),完全一样
以此类推实现第二棵树:
# 拟合第二颗树 # 第一颗预测的结果 gamma = np.array([-0.625]*8 + [2.5]*2) ''' array([-0.625, -0.625, -0.625, -0.625, -0.625, -0.625, -0.625, -0.625, 2.5 , 2.5 ]) ''' # F(x) 随着梯度提升树,提升,发生变化 learning_rate = 0.1 F1 =np.round( F0 + gamma*learning_rate,4) #保留4位小数 ''' array([-0.468 , -0.468 , -0.468 , -0.468 , -0.468 , -0.468 , -0.468 , -0.468 , -0.1555, -0.1555]) ''' # 计算F1(x)的负梯度 yderivative1 = np.round(y - 1/(1 + np.exp(-F1)),4) ''' array([-0.3851, -0.3851, -0.3851, 0.6149, 0.6149, -0.3851, -0.3851, -0.3851, 0.5388, 0.5388]) ''' # 第二颗树分裂标准 mse for i in range(1,11): if i ==10: mse = ((yderivative1 - yderivative1.mean())**2).mean() else: left_mse = ((yderivative1[:i] - yderivative1[:i].mean())**2).mean() right_mse = ((yderivative1[i:] - yderivative1[i:].mean())**2).mean() mse = left_mse*i/10 + right_mse*(10-i)/10 print('从第%d个进行切分'%(i),np.round(mse,4)) # 第二棵树也是从第八个样本这里进行分类,最优的选择,和算法第二颗画图的结果一致 # 左边分支 gamma1 = np.round(yderivative1[:8].sum()/((y[:8] - yderivative1[:8])*(1 - y[:8] + yderivative1[:8])).sum(),3) print('第二棵树左边决策树分支,预测值:',gamma1) # 右边分支 gamma2 =np.round(yderivative1[8:].sum()/((y[8:] - yderivative1[8:])*(1 - y[8:] + yderivative1[8:])).sum(),3) print('第二棵树右边决策树分支,预测值:',gamma2) ''' 第二棵树左边决策树分支,预测值: -0.571 第二棵树右边决策树分支,预测值: 2.168 '''
第三棵树:
# 第二棵树预测值 gamma = np.array([-0.571]*8 + [2.168]*2) # F(x) 随着梯度提升树,提升,发生变化 learning_rate = 0.1 F2 =np.round( F1 + gamma*learning_rate,4) #保留4位小数 # 计算F2(x)的负梯度 yderivative2 = np.round(y - 1/(1 + np.exp(-F2)),4) # 第三颗树分裂标准 mse for i in range(1,11): if i ==10: mse = ((yderivative2 - yderivative2.mean())**2).mean() else: left_mse = ((yderivative2[:i] - yderivative2[:i].mean())**2).mean() right_mse = ((yderivative2[i:] - yderivative2[i:].mean())**2).mean() mse = left_mse*i/10 + right_mse*(10-i)/10 print('从第%d个进行切分'%(i),np.round(mse,4)) # 第三棵树从第三个样本这里进行裂分,最优的选择,和算法第三颗画图的结果一致 # 计算第三颗树的预测值 # 前三个是一类 # 后七个是一类 # 左边分支 gamma1 = np.round(yderivative2[:3].sum()/((y[:3] - yderivative2[:3])*(1 - y[:3] + yderivative2[:3])).sum(),3) print('第三棵树左边决策树分支,预测值:',gamma1) # 右边分支 gamma2 =np.round(yderivative2[3:].sum()/((y[3:] - yderivative2[3:])*(1 - y[3:] + yderivative2[3:])).sum(),3) print('第三棵树右边决策树分支,预测值:',gamma2) ''' 第三棵树左边决策树分支,预测值: -1.592 第三棵树右边决策树分支,预测值: 0.666 '''
最后将最后一棵树的结果通过sigmoid函数转换乘概率:
# 计算第三颗的F3(x) # 第三颗树预测值 gamma = np.array([-1.592]*3 + [0.666]*7) # F(x) 随着梯度提升树,提升,发生变化 learning_rate = 0.1 F3 =np.round( F2 + gamma*learning_rate,4) #保留4位小数 proba = 1/(1 + np.exp(-F3)) # 类别:0,1,如果这个概率大于等于0.5类别1,小于0.5类别0 (proba >= 0.5).astype(np.int8) # 结果 ''' array([0, 0, 0, 0, 0, 0, 0, 0, 1, 1], dtype=int8) '''
可见第三棵树的分类结果已经达到一定的准确率;
以此类推,只要循环的次数足够多, 就能达到和算法的分类结果相同(代码设置的树是100颗)
至此,完毕
三、梯度提升树总结
GBDT的原理是:每一个基模型都会将上一个基模型拟合的残差作为拟合对象,最终累加所有弱分类器的结果作为最终结果。
这里每个基分类器的预测值和实际值的残差 与 最小均方损失函数关于预测值的反向梯度相同
GBDT使用的决策树是CART回归树,无论是处理回归问题还是二分类以及多分类,GBDT使用的决策树通通都是都是CART回归树。为什么不用CART分类树呢?因为GBDT每次迭代要拟合的是梯度值,是连续值所以要用回归树。
四、梯度提升树的优缺点
优点
- 可以灵活处理各种类型的数据,包括连续值和离散值。
- 可以自动进行特征组合,拟合非线性数据;
- 在相对少的调参时间情况下,预测的准确率也可以比较高。这个是相对SVM来说的。
- 使用一些健壮的损失函数,对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
缺点
- 由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
- 对异常点敏感。
五、梯度提升树参数详解
六、与 Adaboost 的对比
相同:
- 都是 Boosting 家族成员,使用弱分类器;
- 都使用前向分布算法;
不同:
- 迭代思路不同:Adaboost 是通过提升错分数据点的权重来弥补模型的不足(利用错分样本),而 GBDT 是通过算梯度来弥补模型的不足(利用残差);
- 损失函数不同:AdaBoost 采用的是指数损失,GBDT 使用的是绝对损失或者 Huber 损失函数;