逻辑回归 | Logistic Regression
1、从线性回归到逻辑回归
我们知道,线性回归的模型是求出输出特征向量 Y 和输入样本矩阵 X 之间的线性关系系数θ,满足Y=Xθ。此时我们的 Y 是连续的,所以是回归模型。如果我们想要 Y 是离散的话,怎么办呢?一个可以想到的办法是,我们对于这个 Y 再做一次函数转换,变为g(Y)。如果我们令g(Y)的值在某个实数区间的时候是类别 A,在另一个实数区间的时候是类别 B,以此类推,就得到了一个分类模型。如果结果的类别只有两种,那么就是一个二元分类模型了。逻辑回归的出发点就是从这来的。下面我们开始引入二元逻辑回归。
2、二元逻辑回归模型
我们提到对线性回归的结果做一个在函数 g 上的转换,可以变化为逻辑回归。这个函数 g 在逻辑回归中我们一般取为 sigmoid 函数,形式如下:
它有一个非常好的性质,即当 z 趋于正无穷时,g(z)趋于 1,而当 z 趋于负无穷时,g(z)趋于 0,这非常适合于我们的分类概率模型。另外,它还有一个很好的导数性质:
如果我们令g(z)中的z为:z=xθ,这样就得到了二元逻辑回归模型的一般形式:
其中x为样本输入,为模型输出,可以理解为某一分类的概率大小。而θ为分类模型的要求出的模型参数。对于模型输出,我们让它和我们的二元样本输出y(假设为0和1)有这样的对应关系,如果 ,即, 则y为1。如果,即, 则y为0。是临界情况,此时, 从逻辑回归模型本身无法确定分类。
的值越小,而分类为0的的概率越高,反之,值越大的话分类为1的的概率越高。如果靠近临界点,则分类准确率会下降。
此处我们也可以将模型写成矩阵模式:
其中为模型输出,为 mx1的维度。X为样本特征矩阵,为mxn的维度。θ为分类的模型系数,为nx1的向量。
3、二元逻辑回归的损失函数
回顾下线性回归的损失函数,由于线性回归是连续的,所以可以使用模型误差的的平方和来定义损失函数。但是逻辑回归不是连续的,自然线性回归损失函数定义的经验就用不上了。不过我们可以用最大似然法来推导出我们的损失函数。
我们知道,按照第二节二元逻辑回归的定义,假设我们的样本输出是 0 或者 1 两类。那么我们有:
两个式子合并得:
其中 y 的取值只能是 0 或者 1。
得到了 y 的概率分布函数表达式,我们就可以用似然函数最大化(最大似然估计)来求解我们需要的模型系数θ。为了方便求解,这里我们用对数似然函数最大化,对数似然函数取反即为我们的损失函数J(θ)
一个样本的似然函数表达式:
m个样本的似然函数表达式:
似然函数对数化,然后取反,即得损失函数:
4、损失函数的优化(梯度下降)
对于二元逻辑回归的损失函数极小化,有比较多的方法,最常见的有梯度下降法,坐标轴下降法,等牛顿法等。本文使用梯度下降法进行优化
损失函数 对 求导:
推导的过程:
求得损失函数的导数之后对 进行梯度更新:
其中 为梯度下降法的步长
5、二元逻辑回归的正则化
逻辑回归也会面临过拟合问题,所以我们也要考虑正则化。常见的有 L1 正则化和 L2 正则化。逻辑回归的 L1 正则化的损失函数表达式如下,相比普通的逻辑回归损失函数,增加了 L1 的范数做作为惩罚,超参数α作为惩罚系数,调节惩罚项的大小。
二元逻辑回归的 L1 正则化损失函数表达式如下:
其中 为θ的 L1 范数。逻辑回归的 L1 正则化损失函数的优化方法常用的有坐标轴下降法和最小角回归法。
二元逻辑回归的 L2 正则化损失函数表达式如下:
为θ的 L2 范数。逻辑回归的 L2 正则化损失函数的优化方法和普通的逻辑回归类似。
6、多元逻辑回归
多元逻辑回归是使用softmax函数来实现多分类的:
softmax函数的计算原理 :
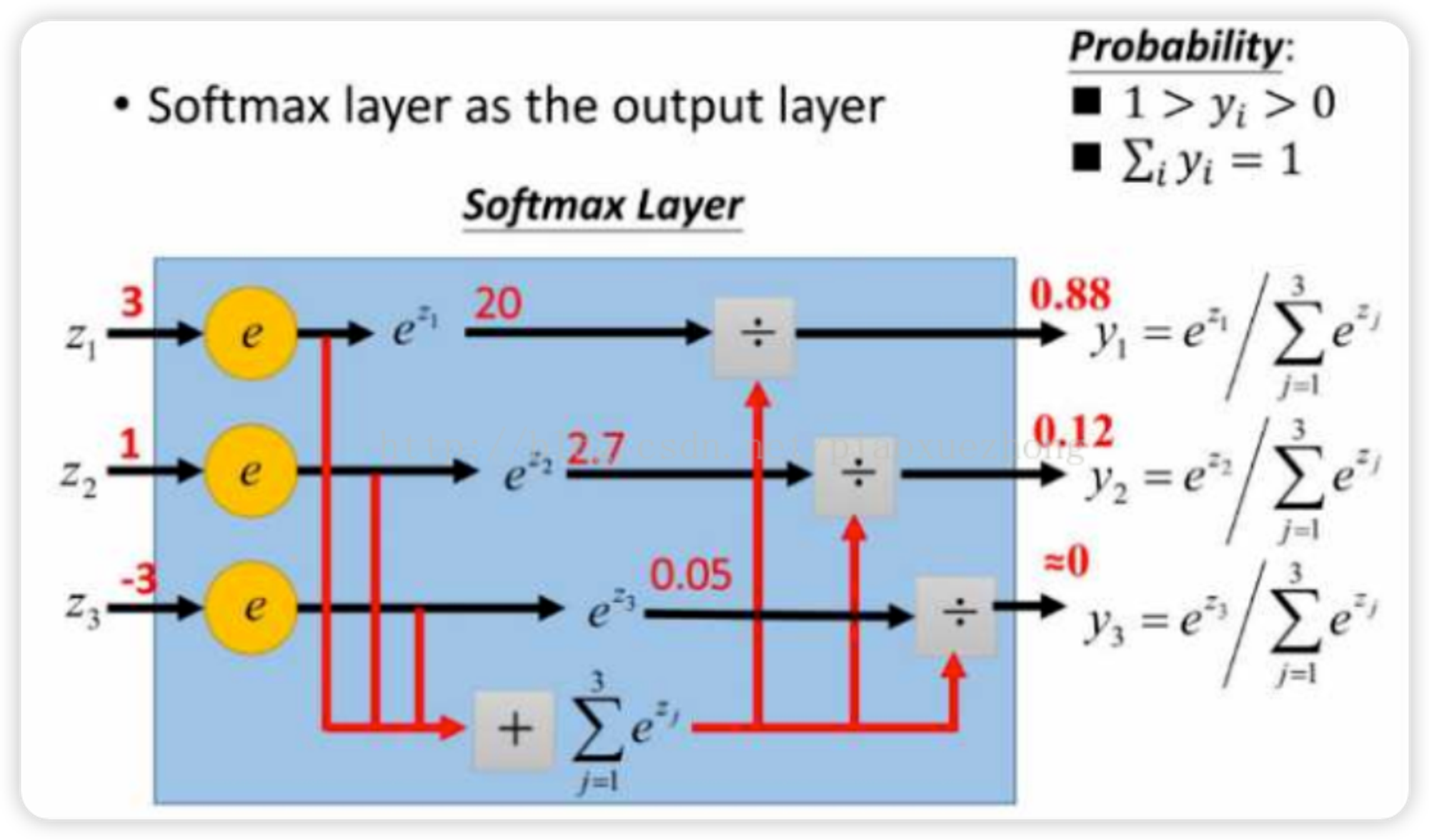
1: 总是认为某种类型为正值,其余为0值,这种方法为最常用的one-vs-rest,简称OvR.
2: 选择一部分类别的样本和另一部分类别的样本来做逻辑回归二分类, 这种方法是Many-vs-Many(MvM)
3: 每次我们选择两类样本来做二元逻辑回归, 这种是One-Vs-One(OvO)。OvO是MvM的特例。
现有n个特征的1个样本, 总的有k个类别:
将得出的k个 值代入softmax函数中转化成总和为1的概率, 选择概率最高的那个分类作为该样本的分类
7、小结
优点
- 容易实现和理解,可解释想很好
- 内存资源占用小,模型训练速度快
- 以概率的形式输出,便利的观测样本概率分数
缺点
- 当特征空间很大时,逻辑回归的性能不是很好;
- 容易欠拟合,一般准确度不太高