OPTICS聚类
type
Post
date
Jul 2, 2020
summary
OPTICS 聚类算法是基于密度的聚类算法,全称是 Ordering points to identify the clustering structure。OPTICS 也是为了优化 DBSCAN 而出现的。
category
学习笔记
tags
聚类
optics
password
URL
Property
Jun 20, 2025 01:47 AM
Optics模型最后的结果会有一个类别为-1,这个类别可以理解为是孤立点,没有被处理到,没有被分类到任何的类别中,可以将其剔除。也可以用来做异常检测。
一、基础理解
OPTICS 聚类算法是基于密度的聚类算法,全称是 Ordering points to identify the clustering structure。提到基于密度的聚类算法,应该很快会想到前面介绍的 DBSCAN 聚类算法,事实上,OPTICS 也是为了优化 DBSCAN 而出现的。
在 DBSCAN 算法中,有两个比较重要的参数:邻域半径 eps 和核心对象的最小邻域样本数 min_samples,选择不同的参数会导致最终聚类的结果千差万别,而在高维数据中,两个参数的联合调参也不是一件容易的事。OPTICS 算法的提出就是为了帮助 DBSCAN 算法选择合适的参数,降低输入参数的敏感度。实际上,OPTICS 并不显式的生成数据聚类结果,只是对数据集中的对象进行排序,得到一个有序的对象列表,通过该有序列表,可以得到一个决策图,通过决策图可以选择不同的 eps 参数进行 DBSCAN 聚类。在继续阅读下面的内容之前,需要先了解 DBSCAN 的相关内容,因为本文的部分概念来自于 DBSCAN。
在 DBSCAN 的基础上,OPTICS 定义了两个新的距离概念:
(1)核心距离
对于一个给定的核心对象 X,使得 X 成为核心对象的最小邻域距离 r 就是 X 的核心距离。这句话乍一看有点绕,其实仔细读两遍就明白了,假如在 DBSCAN 中我们定义 eps = 1.2 和 min_samples=5,X 在 eps = 1.2 的邻域内有 8 个样本点,则 X 是核心对象,但是我们发现距离 X 最近的第 5 个点和 X 的距离是 0.8,那么核心对象 X 的核心距离就是 0.8,显然每个核心对象的核心距离并不都是相同的。参考图 1,注意在计算 min_samples 的时候,一般也包括样本点自身,所以只需在 P 点 eps 邻域内找到 7 个点,那么 P 点就是核心点。
(2)可达距离
如果 X 是核心对象,则对象 Y 到对象 X 的可达距离就是 Y 到 X 的欧氏距离和 X 的核心距离的最大值,如果 X 不是核心对象,则 Y 和 X 之间的可达距离就没有意义(不存在可达距离),显然,数据集中有多少核心对象,那么 Y 就有多少个可达距离。在下文介绍 API 的时候,我们会介绍在 OPTICS 中,一般默认设置 eps 为无穷大,即只要数据集的样本数不少于 min_samples,那么任意一个样本点都是核心对象,即都有核心距离,且任意两个对象之间都存在可达距离。
图 1
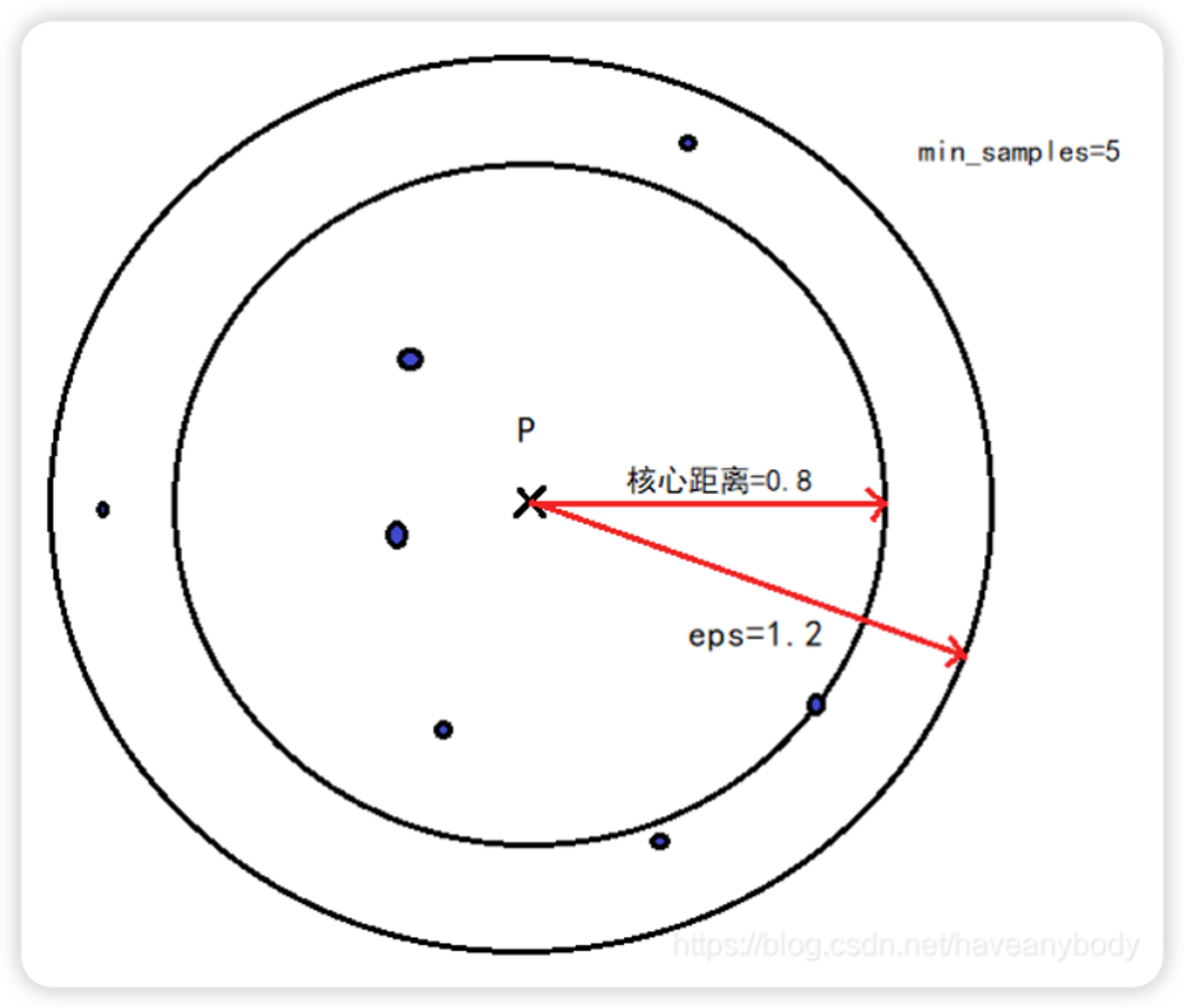
二、算法原理
OPTICS 的原理并不复杂,只不过大多数介绍资料都喜欢列举一些广义的算法流程或者伪代码,虽然满足算法介绍的严谨性,但是阅读起来不免显得晦涩难懂,没有阅读的欲望。因此,和之前的文章一样,本文也是先介绍 OPTICS 的标准算法流程,然后再以案例的形式介绍流程的具体执行逻辑,如果算法流程不能一下子理解的话,可以先跳过直接看后面的案例,然后再回来看标准流程。
OPTICS 算法流程:
- 已知数据集 D,创建两个队列,有序队列 O 和结果队列 R(有序队列用来存储核心对象及其该核心对象的密度直达对象,并按可达距离升序排列;结果队列用来存储样本点的输出次序。可以把有序队列里面放的理解为待处理的数据,而结果队列里放的是已经处理完的数据)。
- 如果 D 中所有点都处理完毕或者不存在核心点,则算法结束。否则,选择一个未处理(即不在结果队列 R 中)且为核心对象的样本点 p,首先将 p 放入结果队列 R 中,并从 D 中删除 p。然后找到 D 中 p 的所有密度直达样本点 x,计算 x 到 p 的可达距离,如果 x 不在有序队列 O 中,则将 x 以及可达距离放入 O 中,若 x 在 O 中,则如果 x 新的可达距离更小,则更新 x 的可达距离,最后对 O 中数据按可达距离从小到大重新排序。
- 如果有序队列 O 为空,则回到步骤 2,否则取出 O 中第一个样本点 y(即可达距离最小的样本点),放入 R 中,并从 D 和 O 中删除 y。如果 y 不是核心对象,则重复步骤 3(即找 O 中剩余数据可达距离最小的样本点);如果 y 是核心对象,则找到 y 在 D 中的所有密度直达样本点,并计算到 y 的可达距离,然后按照步骤 2 将所有 y 的密度直达样本点更新到 O 中。
- 重复步骤 2、3,直到算法结束。最终可以得到一个有序的输出结果,以及相应的可达距离。
三、数据实例
3.1、手动推导
已知样本数据集为:D = {[1, 2], [2, 5], [8, 7], [3, 6], [8, 8], [7, 3], [4,5]},为了更好地标识索引,我们以表格标识数据如下:
图 2
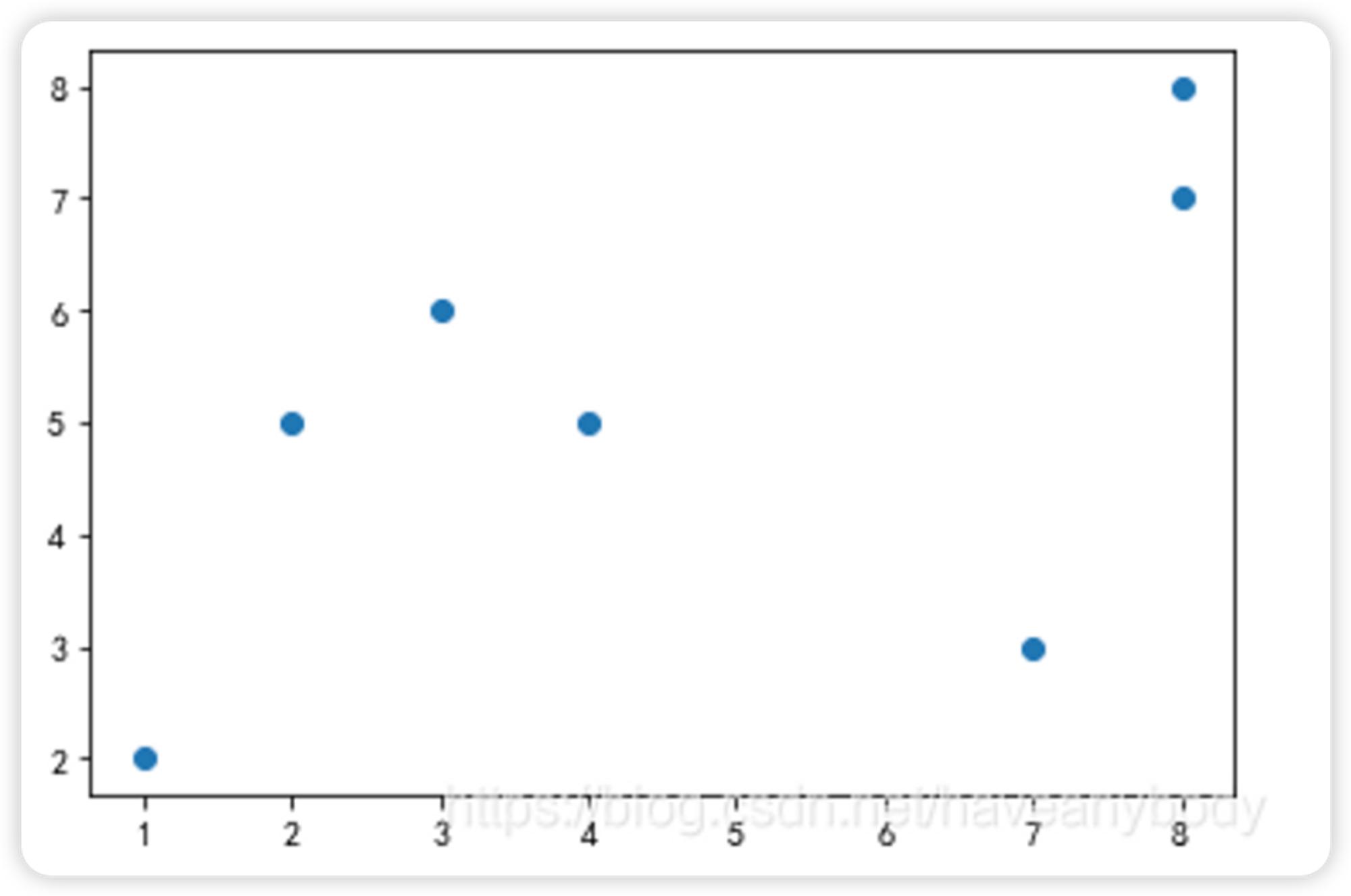
索引 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 核心对象 |
元素 | (1, 2) | (2, 5) | (8, 7) | (3, 6) | (8, 8) | (7, 3) | (4, 5) | 0 |
核心距离 | 3.16 | 1.41 | 1.0 | 1.41 | 1.0 | 3.61 | 1.41 | 0 |
第一次可达距离 | inf | 3.16 | 8.60 | 4.47 | 9.21 | 6.08 | 4.24 | 0 |
第二次可达距离 | -- | -- | 6.32 | 1.41 | 6.70 | 5.38 | 2.0 | 1 |
第三次可达距离 | -- | -- | 5.09 | -- | 5.39 | 5.0 | 1.41 | 3 |
第四次可达距离 | -- | -- | 4.47 | -- | 5.0 | 3.61 | -- | 6 |
第五次可达距离 | -- | -- | 4.12 | -- | 5.0
(5.10) | -- | -- | 5 |
第六次可达距离 | -- | -- | -- | -- | 1.0 | -- | -- | 2 |
输出顺序 | 0 | 1 | 5 | 2 | 6 | 4 | 3 | 0 |
可达距离 | inf | 3.16 | 4.12 | 1.41 | 1.0 | 3.61 | 1.41 | 0 |
假设 eps = inf,min_samples=2,则数据集 D 在 OPTICS 算法上的执行步骤如下:
- 计算所有的核心对象和核心距离,因为 eps 为无穷大,则显然每个样本点都是核心对象。因为 min_samples=2,则每个核心对象的核心距离就是离自己最近样本点到自己的距离(样本点自身也是邻域元素之一),具体如上表所示。
- 随机在 D 中选择一个核心对象,假设选择 0 号元素,将 0 号元素放入 R 中,并从 D 中删除。因为 eps = inf,则其他所有样本点都是 0 号元素的密度直达对象,计算其他所有元素到 0 号元素的可达距离(实际就是计算所有元素到 0 号元素的欧氏距离,如表 1 第一次可达距离),并按可达距离排序,添加到序列 O 中。
- 此时 O 中可达距离最小的元素是 1 号元素,取出 1 号元素放入 R ,并从 D 和 O 中删除,因为 1 号元素是核心对象,找到 1 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表 1 第二次可达距离)。
- 此时 O 中可达距离最小的元素是 3 号元素,取出 3 号元素放入 R ,并从 D 和 O 中删除,因为 3 号元素是核心对象,找到 3 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表 1 第三次可达距离)。
- 此时 O 中可达距离最小的元素是 6 号元素,取出 6 号元素放入 R ,并从 D 和 O 中删除,因为 6 号元素是核心对象,找到 6 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表 1 第四次可达距离)。
- 此时 O 中可达距离最小的元素是 5 号元素,取出 5 号元素放入 R ,并从 D 和 O 中删除,因为 5 号元素是核心对象,找到 5 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表 1 第五次可达距离)。注意本次计算的 4 号元素到 5 号元素的可达距离是 5.10,大于 5.0,因此不更新 4 号元素的可达距离(此处存疑)。
- 此时 O 中可达距离最小的元素是 2 号元素,取出 2 号元素放入 R ,并从 D 和 O 中删除,因为 2 号元素是核心对象,找到 2 号元素在 D 中的所有密度直达对象(剩余的所有样本点),并计算可达距离,同时更新 O(如表 1 第六次可达距离)。
- 此时 O 中可达距离最小的元素是 4 号元素,取出 4 号元素放入 R ,并从 D 和 O 中删除,因为 D 已空,O 也已空,程序结束。根据表 1,最终的结果序列 R 的元素索引输出顺序为:0、1、3、6、5、2、4,可达距离如表 1 最后一行所示。
我们按照最终的输出顺序绘制可达距离图(注意,因为第一个元素没有可达距离,或者说可达距离是无穷大,故图中没有标出 0 号元素的可达距离):
图 3
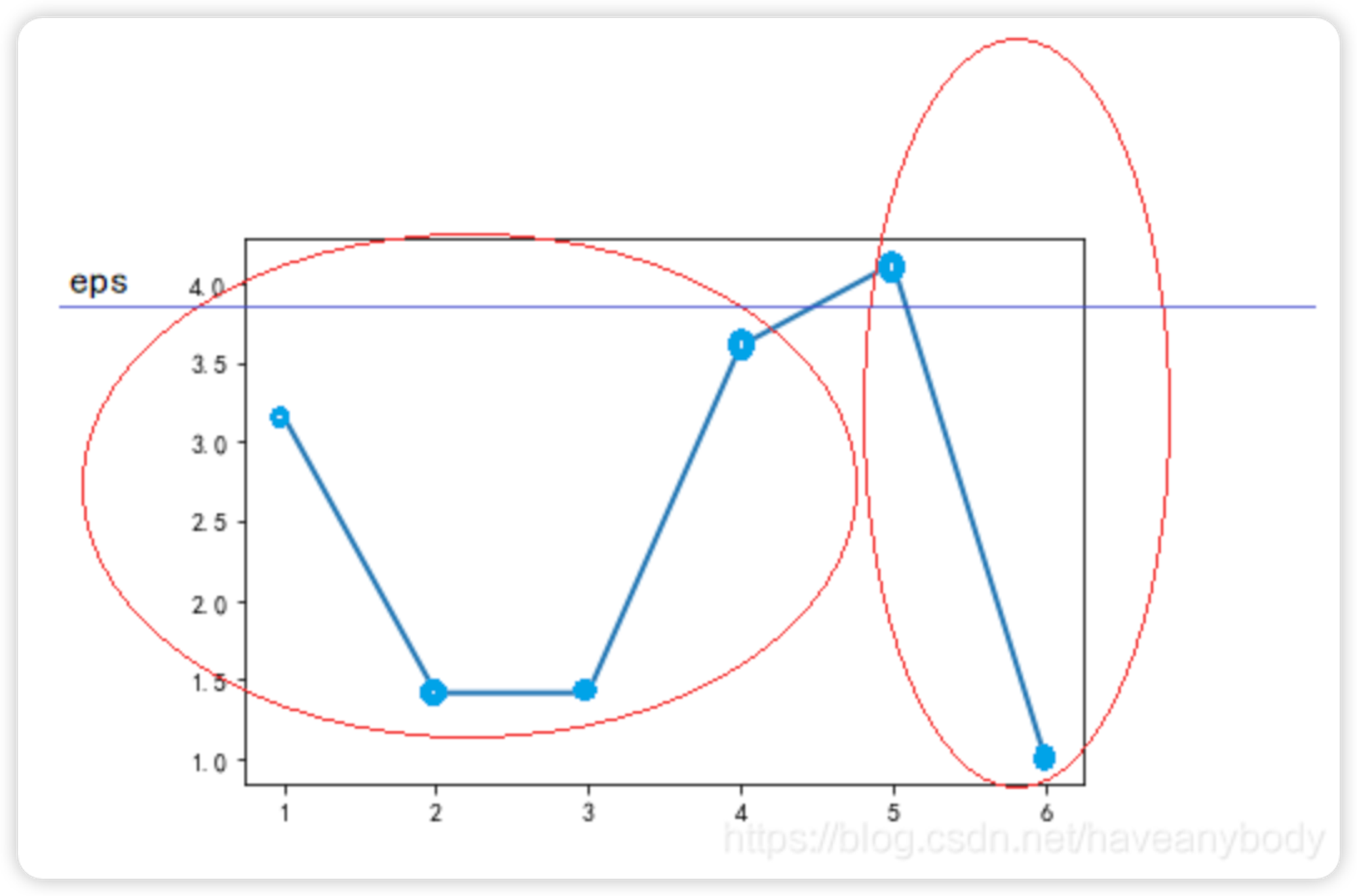
可以发现,可达距离呈现两个波谷,也即表现为两个簇,波谷越深,表示簇越紧密,只需要在两个波谷之间取一个合适的 eps 分隔值(图中蓝色的直线,例如两个可达距离的平均值),得到合适的eps之后(上面这个图只能用来确定eps值,不是用来划分的),使用 DBSCAN 算法就会聚类为两个簇。即第一个簇的元素为:0、1、3、6、5;第二个簇的元素为:2、4。
用python实现以上推打过程:
from cmath import inf from math import sqrt import random import matplotlib.pyplot as plt eps = inf # 默认核心距离无穷大,则每个点都是核心点 min_sample = 2 # 默认最小邻域样本数为2,核心距离就是离自己最近样本点到自己的距离(样本点自身也是邻域元素之一) D = [[1, 2], [2, 5], [8, 7], [3, 6], [8, 8], [7, 3], [4,5]] print("原数据D:", D) O = [] # 排序队列 R = [] # 结果队列 S = [] # 可达距离 R.append(D.pop(random.randint(0,6))) # 第一轮随机取 print("第1轮R:", R) nums = 1 while True: if len(D)<=0: break else: O = [] # 排序队列 for x in D: # 计算R中的点与D中其他点的距离,并按距离升序 x_d = sqrt((R[-1][0] - x[0])**2 + (R[-1][1] - x[1])**2) O.append([x, x_d]) O = sorted(O, key=lambda x: x[1], reverse=False) print(f"第{nums}轮O:", O) S.append(round(O[0][1],2)) print(f"第{nums}轮S:", S) D.remove(O[0][0]) # 将距离最小的点从D中删除 print(f"第{nums+1}轮D:", D) R.append(O[0][0]) # 将距离最小的点加到R中 print(f"第{nums+1}轮R:", R) nums+=1 plt.plot(range(len(S)), S, 'ro-') plt.show()
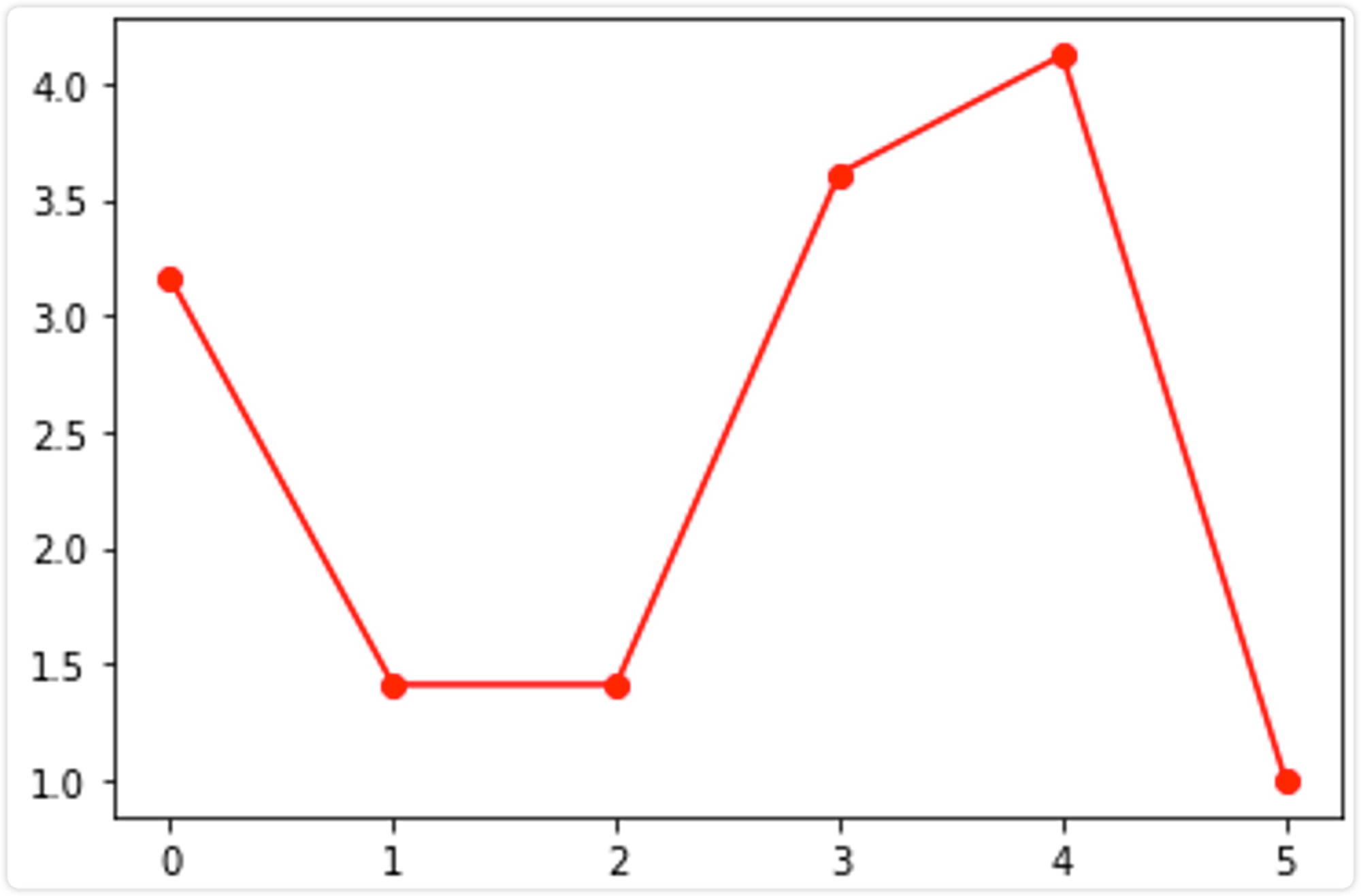
下面我们通过 sklearn 库来验证我们的结果。
sklearn 库同样为我们封装了 OPTICS 算法的 API,供我们直接使用。
3.2、使用算法验证
基于 1.1 的数据集,使用 OPTICS 验证算法结果如下:
from sklearn.cluster import OPTICS import numpy as np X = np.array([[1, 2], [2, 5], [8, 7],[3, 6], [8, 8], [7, 3], [4,5]]) clustering = OPTICS(min_samples=2).fit(X) print(clustering.core_distances_) ''' array([3.16227766, 1.41421356, 1. , 1.41421356, 1. ,3.60555128, 1.41421356]) ''' print(clustering.ordering_) ''' array([0, 1, 3, 6, 5, 2, 4]) ''' print(clustering.reachability_) ''' array([inf, 3.16227766, 4.12310563, 1.41421356, 1. ,3.60555128, 1.41421356]) ''' print(clustering.labels_) ''' array([0, 0, 1, 0, 1, 0, 0]) '''
根据图 3,选择 eps=3.8,使用 DBSCAN 算法验证如下:
import sklearn db = sklearn.cluster.DBSCAN(eps=3.8,min_samples=2).fit(X) db.labels_ ## array([0, 0, 1, 0, 1, 0, 0])
四、API调用
4.1、算法参数详解
from sklearn.cluster import OPTICS OPTICS(*, min_samples=5, max_eps=inf, metric='minkowski', p=2, metric_params=None, cluster_method='xi', eps=None, xi=0.05, predecessor_correction=True, min_cluster_size=None, algorithm='auto', leaf_size=30, n_jobs=None)
参数 | 说明 |
min_samples | int > 1 or float between 0 and 1 (default=5)
经验理解:每个类别应包含的最少样本数
官方解释:一个点被视为核心点的邻域样本数。此外,上下陡峭地区不能有超过 min_samples连续的非陡峭点。表示为样本数的绝对值或一小部分(四舍五入至少为2)。 |
max_eps | float, optional (default=np.inf)两个样本之间的最大距离,其中一个被视为另一个样本的邻域。 np.inf默认值将识别所有规模的聚类;减少max_eps会缩短运行时间。 |
metric | str or callable, optional (default=’minkowski’)用于距离计算的度量。任何来自scikit-learn或scipy.spatial.distance的度量都可以使用。如果度量是可调用的函数,则在每对实例(行)上调用它,并记录结果值。可调用应该以两个数组作为输入,并返回一个值,指示它们之间的距离。这适用于Scipy’s度量,但比将度量名称作为字符串传递的效率要低。如果度量是“precomputed”,则假定X是距离矩阵,并且必须是平方的。度量的有效值是:scikit-learn里面:[‘cityblock’, ‘cosine’, ‘euclidean’, ‘l1’, ‘l2’, ‘manhattan’]scipy.spatial.distance里面:[‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘correlation’, ‘dice’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘yule’]有关这些度量的详细信息,请参阅scipy.spatial.distance的文档。 |
p | int, optional (default=2)来自 sklearn.metrics.pairwise_distances的Minkowski度量的参数。当p=1时,这相当于使用曼哈顿距离(L1); 当p=2, 相当于使用欧几里得距离(L2)。对于任意p,使用minkowski_distance (l_p)。 |
metric_params | dict, optional (default=None)度量函数的附加关键字参数。 |
cluster_method | str, optional (default=’xi’)利用计算的可达性和有序性提取簇的提取方法,可能的值是“xi”和“dbscan”。 |
eps | float, optional (default=None)两个样本之间的最大距离,其中一个被视为另一个样本的邻域内。默认情况下,它假设的值与 max_eps相同。只有当cluster_method='dbscan'才被使用。 |
xi | float, between 0 and 1, optional (default=0.05)确定构成聚类边界的可达性图的最小陡度。例如,可达图中的一个向上点定义为从一个点到它的后继点最多为1-xi的比率。只有当 cluster_method='xi'才被使用。 |
predecessor_correction | bool, optional (default=True)根据OPTICS预先计算的[R2c55e37003fe-2]正确的团簇。此参数对大多数数据集的影响最小。只有当 cluster_method='xi'才被使用。 |
min_cluster_size | int > 1 or float between 0 and 1 (default=None)OPTICS聚类中的最小样本数,表示为样本数的绝对值或一部分(四舍五入为至少2)。如果为None, min_samples的值将被使用。只有当cluster_method='xi'才被使用。 |
algorithm | {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’NearestNeighbors模块用于计算点态距离和寻找最近邻的算法。 |
p | float, default=None 用于计算点间距离的Minkowski度量的幂。- ‘ball_tree’将会使用 BallTree- ‘kd_tree’将会使用KDtree- ‘brute’将会使用蛮力搜索- ‘auto’将尝试根据传递给fit方法的值来确定最合适的算法。(默认) |
n_jobs | int or None, optional (default=None)要为邻居搜索的并行作业数。 None意味1, 除非在joblib.parallel_backend环境中。-1指使用所有处理器。有关详细信息,请参Glossary。 |
属性 | 说明 |
labels_ | array, shape (n_samples,)为fit()提供的数据集中每个点的聚类标签。不包含在 cluster_hierarchy_的叶簇中的含噪样本和点被标记为-1。 |
reachability_ | array, shape (n_samples,)每个样本的可达距离,按对象顺序索引。使用 clust.achaability_[clust.order_]按聚类顺序访问。 |
ordering_ | array, shape (n_samples,)样本索引的聚类排序列表。 |
core_distances_ | array, shape (n_samples,)每个样本成为一个核心点的距离,按对象顺序索引。有一个inf的距离点永远不会成为核心。使用 clust.core_distances_[clust.ordering_]按聚类排序进行访问。 |
predecessor_ | array, shape (n_samples,)指出一个样本是从中得到的,并按对象顺序进行索引。种子点有-1的前身。 |
cluster_hierarchy_ | array, shape (n_clusters, 2)每一行中 [start,end]形式的聚类列表,包括所有索引。聚类按照(end, -start)(升序)排列,这样包含较小的簇的更大的簇就在那些较小的簇之后。由于标签不反映层次结构,通常len(cluster_hierarchy_) > np.unique(optics.labels_)。请注意这些索引是ordering_。即X[ordering_][start:end + 1]形成成一个簇。只有当cluster_method='xi'才被使用。 |
方法 | 说明 |
fit(self, X[, y]) | 执行OPTICS聚类 |
fit_predict(self, X[, y]) | 在X上执行聚类并返回聚类标签 |
get_params(self[, deep]) | 获取此估计器的参数 |
set_params(self, **params) | 设置此估计器的参数 |