机器学习常用算法调用集合
type
Post
date
May 31, 2023
summary
这是一篇算法调用集合整理,搜集了一些常用的机器学习算法的调用方式、参数详解、调参方法和实例。仅供学习、记录和快速查询,内容还在持续更新中。
category
学习笔记
tags
模型调用
调参
Sklearn
password
URL
Property
Jun 20, 2025 01:47 AM
先放上大名鼎鼎的算法选择图
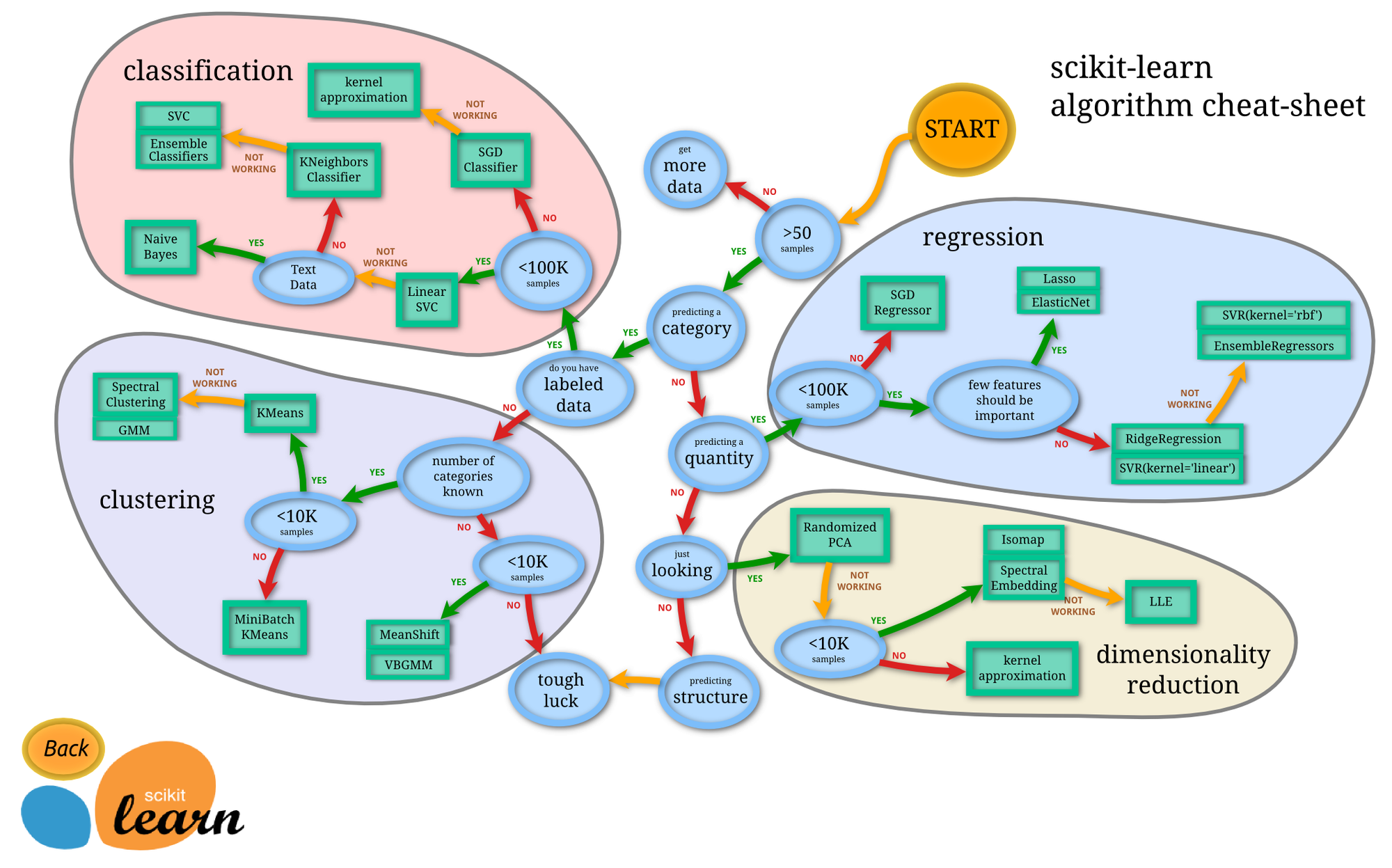
一、分类算法
from sklearn.linear_model import Ridge # 岭回归 from sklearn.linear_model import Lasso # 套索回归 from sklearn.linear_model import LinearRegression # 线性回归 from sklearn.linear_model import LogisticRegression # 逻辑斯蒂 from sklearn.tree import DecisionTreeClassifier # 决策树--分类 from sklearn.tree import DecisionTreeRegressor # 决策树--回归 from sklearn.ensemble import RandomForestClassifier # 随机森林--分类 from sklearn.ensemble import RandomForestRegressor # 随机森林--回归 from sklearn.ensemble import GradientBoostingClassifier # GBDT--分类 from sklearn.ensemble import GradientBoostingRegressor # GBDT--回归 import xgboost as gbt from xgboost import XGBClassifier # XGBoost import lightgbm as lgbm from lightgbm import LGBMClassifier # LightGBM from sklearn.svm import SVC # 支持向量机--分类 from sklearn.svm import SVR # 支持向量机--回归 from sklearn.neighbors import KNeighborsClassifier # KNN--分类 from sklearn.neighbors import KNeighborsRegressor # KNN--回归 from sklearn.neural_network import MLPClassifier # 多层感知机
1.1、逻辑回归
1.1.1、示例&调参
from sklearn.linear_model import LogisticRegression # 逻辑斯蒂(人为指定一个正则化系数) from sklearn.linear_model import LogisticRegressionCV # 逻辑斯蒂(使用交叉验证来选择正则化系数C,用法大致相同) from sklearn.model_selection import GridSearchCV # 网格搜索 clf_lr = LogisticRegression() # 定义模型实例 clf_lr.fit(X, y) # 训练模型 clf_lr.predict(X) # 样本对应各个类别预测标签 param_grid = {"penalty":['l1', 'l2'], "C":[0.01, 0.1, 1, 10, 100]} grid_search_lr = GridSearchCV(clf_lr, param_grid, cv=5, scoring='neg_log_loss') grid_search_lr.fit(X, y) grid_search_lr.best_score_ # 获取最高分 grid_search_lr.best_params_ # 获取被搜索的最好参数 grid_search_lr.best_estimator_ # 获取最佳估计器(带所有参数的值)
1.1.2、参数详解(部分)
参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
penalty | 正则化项 | l2 | str | None
l1:l1正则化
l2:l2正则化
elasticnet:l1+l2 | 解决过拟合选择l2,如果还是过拟合再选择l1
特征多时,想要不重要的特征系数归零让系数稀疏化,选择l1 |
C | 正则化系数λ的倒数 | 1 | positive float | ㅤ | 值越小正则化越强 |
class_weight | 类别权重 | None | dict or str | 自定义字典或balanced | 自定义:class_weight={0:0.9, 1:0.1};自动计算:‘balanced’ |
random_state | 随机数种子 | None | int | ㅤ | 仅在正则化优化算法为sag,liblinear时有用 |
solver | 优化算法 | lbfgs | str | liblinear:基于开源的liblinear库实现
lbfgs:拟牛顿法的一种;
newton-cg:拟牛顿法的一种;
sag:随机平均梯度下降;
saga:线性收敛的随机优化算法; | 对于小型数据集:可以选择‘liblinear’,
对于大型数据集(10w+):’sag’和’saga’
对于多分类问题:’newton-cg’,‘sag’,'saga’,’lbfgs’
只能处理L2惩罚:‘newton-cg’、'lbfgs’和’sag’
处理L1和L2惩罚:’liblinear’和’saga’ |
tol | 停止优化的误差容忍度 | 1e-4 | float | ㅤ | 值越小,精度越高,但是训练时间也可能随之增加。 |
max_iter | 最大迭代次数 | 100 | int | ㅤ | 仅适用于newton-cg,sag和lbfgs求解器 |
multi_class | 分类方式 | ovr | str | ovr:选一类为正,进行二分类
multinomial:选多类为正,进行二分类 | 二分类,选哪个无所谓
多分,ovr速度快效果略差 |
verbose | 输出日志 | 0 | int | 0、1 | ㅤ |
n_jobs | 工作核数 | 1 | int | ㅤ | -1,使用所有可用核心 |
模型方法
clf_lr.fit(X, y) # 训练模型 clf_lr.get_params([deep]) # 获取模型参数 clf_lr.predict(X) # 样本对应各个类别预测标签 clf_lr.predict_proba(X) # 样本对应各个类别的概率 clf_lr.predict_log_proba(X) # 样本对应各个类别的概率的对数转化 clf_lr.score(X, y) # 模型预测得分(官方文档描述是accuracy准确率)
1.2、随机森林
1.2.1、示例&调参
from sklearn.ensemble import RandomForestClassifier # 随机森林 from sklearn.model_selection import GridSearchCV # 网格搜索 clf_rf = RandomForestClassifier() # 定义模型实例 clf_rf.fit(X, y) # 训练模型 clf_rf.predict(X) # 样本对应各个类别预测标签 clf_lr.predict_proba(X) # 样本对应各个类别的概率 param_grid = {'n_estimators':range(10,71,10), 'max_features':range(3,11,2), 'max_depth':range(3,14,2), 'min_samples_split':range(80,150,20), 'min_samples_leaf':range(10,60,10)} grid_search_rf = GridSearchCV(clf_rf, param_grid = param_grid, scoring='roc_auc',cv=5) grid_search_rf.fit(X,y) grid_search_rf.best_score_ # 获取最高分 grid_search_rf.best_params_ # 获取被搜索的最好参数 grid_search_rf.best_estimator_ # 获取最佳估计器(带所有参数的值)
1.2.2、参数详解(部分)
参数类型 | 参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
框架参数 | n_estimators | 树的棵数 | l00 | int | ㅤ | 太小容易欠拟合,太大加大计算量,临界值后提升会很小 |
框架参数 | criterion | 决策树算法 | gini | str | gini:基尼系数,CART算法
entropy:信息熵,ID3 算法
log_loss:对数损失,同entropy | 推荐默认 |
框架参数 | oob_score | 是否采用袋外样本来评估模型 | False | bool | True、False | 条件允许的话设置为True |
决策树参数 | max_depth | 树的最大深度 | None | int | ㅤ | ㅤ |
决策树参数 | max_features | 树划分时最大特征数 | sqrt | str or int or float | int:整数n个特征
float:n_features * float 个特征
auto:sqrt(n_features)
sqrt:sqrt(n_features),同上
log2:log2(n_features)
None | 推荐默认 |
决策树参数 | min_samples_split | 分割内部节点所需最小样本数 | 2 | int or float | int:整数n个样本
float:n_sample * float 个样本 | 如果样本量数量级非常大,则推荐增大这个值。 |
决策树参数 | min_samples_leaf | 分割叶子节点所需最少样本数 | 1 | int or float | int:整数n个样本
float:n_sample * float 个样本 | 如果样本量数量级非常大,则推荐增大这个值。 |
决策树参数 | bootstrap | 是否有放回采样 | True | bool | True、False | ㅤ |
决策树参数 | n_jobs | 工作核数 | 1 | int | ㅤ | -1,使用所有可用核心 |
1.3、GBDT
1.3.1、示例&调参
from sklearn.ensemble import GradientBoostingClassifier # GBDT--分类 from sklearn.ensemble import GradientBoostingRegressor # GBDT--回归 from sklearn.model_selection import GridSearchCV # 网格搜索 clf_gbdt = GradientBoostingClassifier() # 定义模型实例 clf_gbdt.fit(X, y) # 训练模型 clf_gbdt.predict(X) # 样本对应各个类别预测标签 clf_gbdt.predict_proba(X) # 样本对应各个类别的概率 param_grid = {'n_estimators':range(20,81,10), 'learning_rate':[0.01, 0.05,0.1,0.5], 'max_depth':range(3,14,2), 'min_samples_split':range(100,801,200), 'min_samples_leaf':range(60,101,10), 'max_features':range(3,11,2), 'subsample':[0.6,0.7,0.75,0.8,0.85,0.9]} grid_search_gbdt = GridSearchCV(clf_gbdt, param_grid = param_grid, scoring='roc_auc',cv=5) grid_search_gbdt.fit(X,y) grid_search_gbdt.best_score_ # 获取最高分 grid_search_gbdt.best_params_ # 获取被搜索的最好参数 grid_search_gbdt.best_estimator_ # 获取最佳估计器(带所有参数的值)
1.3.2、参数详解(部分)
参数类型 | 参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
框架参数 | n_estimators | 弱学习器的最大迭代次数 | 100 | int | ㅤ | ㅤ |
框架参数 | learning_rate | 学习率 | 0.1 | float | (0,1] | 通常我们用步长和迭代最大次数一起来决定算法的拟合效果 |
框架参数 | subsample | 子采样样本比例 | 1 | float | (0,1] | 随机森林使用的是放回抽样,而这里是不放回抽样
推荐在[0.5, 0.8]之间,默认是1.0,即不使用子采样 |
框架参数 | init | ㅤ | ㅤ | ㅤ | ㅤ | 没看懂,可以不用管 |
框架参数 | criterion | 划分子树的评估标准 | friedman_mse | str | friedman_mse
squared_error | 推荐默认 |
框架参数 | loss | 损失函数 | log_loss | str | log_loss:对数损失
deviance:似然损失函数
exponential:指数损失函数 | 指数损失函数等于把我们带到了Adaboost算法 |
弱学习器参数 | max_depth | 树的最大深度 | 3 | int | ㅤ | [3, 5, 8, 15, 25, 30, None] |
弱学习器参数 | max_features | 树划分时最大特征数 | sqrt | str or int or float | int:整数n个特征
float:n_features * float 个特征
auto:sqrt(n_features)
sqrt:sqrt(n_features),同上
log2:log2(n_features)
None | 推荐默认
特征小于50,用"None"就可以了 |
弱学习器参数 | min_samples_split | 分割内部节点所需最小样本数 | 2 | int or float | int:整数n个样本
float:n_sample * float 个样本 | 如果样本量数量级非常大,则推荐增大这个值。
[1, 2, 5, 10, 15, 100] |
弱学习器参数 | min_samples_leaf | 分割叶子节点所需最少样本数 | 1 | int or float | int:整数n个样本
float:n_sample * float 个样本 | 如果样本量数量级非常大,则推荐增大这个值。
[1, 2, 5, 10] |
弱学习器参数 | min_weight_fraction_leaf | 叶子节点最小的样本权重和 | 0 | float | [0.0, 0.5] | ㅤ |
弱学习器参数 | max_leaf_nodes | 最大叶子节点数 | None | int | [2, inf) | ㅤ |
1.4、XGBoost
1.5、LightGBM
1.5.1、接口调用
1.5.1.1、原生接口调用
# import lightgbm as lgb from lightgbm import plot_importance from sklearn.datasets import load_iris from sklearn.metrics import accuracy_score from sklearn.model_selection import train_test_split lightgbm.train(params, train_set, num_boost_round=100, valid_sets=None, valid_names=None, fobj=None, feval=None, init_model=None, feature_name='auto', categorical_feature='auto', early_stopping_rounds=None, evals_result=None, verbose_eval=True, learning_rates=None, keep_training_booster=False, callbacks=None) """ params:参数 train_set:训练数据,需要用特定方式转换,详见下文 num_boost_round:最大迭代次数,默认10 valid_sets:用于评估的数据及数据的名称,列表类型, fobj:指定二阶可导的自定义目标函数 feval:自定义评估函数 categorical_feature:指定哪些是类别特征 early_stopping_rounds:指定迭代多少次没有得到优化则停止训练,默认值为None,表示不提前停止训练。 verbose_eval:可以是bool类型,也可以是整数类型。如果设置为整数,则每间隔verbose_eval次迭代就输出一次信息。 init_model:加载之前训练好的 lgb 模型,用于增量训练。 """ # 加载鸢尾花数据集 iris = load_iris() X,y = iris.data,iris.target # 数据集分割 X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=123457) # 构造训练集 dtrain = lgb.Dataset(X_train,y_train) dtest = lgb.Dataset(X_test,y_test) # 参数 params = { 'booster': 'gbtree', 'objective': 'multiclass', 'num_class': 3, 'num_leaves': 31, 'subsample': 0.8, 'bagging_freq': 1, 'feature_fraction ': 0.8, 'slient': 1, 'learning_rate ': 0.01, 'seed': 0 } # xgboost模型训练 model = lgb.train(params,dtrain, num_boost_round=100, valid_sets=[dtrain, dtest], verbose_eval=100, early_stopping_rounds=30) # 对测试集进行预测 y_pred = model.predict(X_test) # 计算准确率 accuracy = accuracy_score(y_test, np.argmax(y_pred, axis=1)) print('accuarcy:%.2f%%'%(accuracy*100)) # 显示重要特征 plot_importance(model)
1.5.1.2、sklearn风格接口调用
import matplotlib.pyplot as plt from lightgbm import LGBMClassifier from lightgbm import plot_importance from sklearn.datasets import load_iris from sklearn.metrics import accuracy_score from sklearn.model_selection import train_test_split # 加载样本数据集 iris = load_iris() X,y = iris.data,iris.target X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=12343) crf_lgbm = LGBMClassifier( max_depth=3, learning_rate=0.1, n_estimators=200, # 使用多少个弱分类器 objective='multiclass', num_class=3, booster='gbtree', min_child_weight=2, subsample=0.8, colsample_bytree=0.8, reg_alpha=0, reg_lambda=1, seed=0 # 随机数种子 ) crf_lgbm.fit(X_train,y_train, eval_set=[(X_train, y_train), (X_test, y_test)], # [(X_test, y_test)] verbose=100, early_stopping_rounds=50) # 对测试集进行预测 y_pred = crf_lgbm.predict(X_test) y_proba = crf_lgbm.predict_proba(X_test) # 计算平均 auc n_classes = y_true.shape[1] # 类别数 auc_scores = [] # 存储每个二分类子问题的AUC值 for i in range(n_classes): y_true_binary = np.array(pd.get_dummies(y_test))[:, i] # 将第i个类别设为正例,将标签独热编码 y_pred_binary = y_proba[:, i] # 第i个类别的预测概率或分数 # 计算第i个二分类子问题的AUC值 auc = roc_auc_score(y_true_binary, y_pred_binary) auc_scores.append(auc) # 计算AUCµ的值 auc_micro = np.mean(auc_scores) #计算准确率 accuracy = accuracy_score(y_test,y_pred) print('accuracy:%3.f%%'%(accuracy*100)) # 显示重要特征 plot_importance(model) plt.show()
1.5.2、参数详解
参数类型 | 参数 | 含义 | 功能 | 默认值 | 类型 | 可选项 | 选择经验 |
根据场景确定 | objective | 学习目标 | 指定任务类型 | regression | str or None | regression:L2正则项的回归(回归)
regression_l1:L1正则项的回归(回归)
mape:平均绝对百分比误差(回归)
binary:二分类 log loss(分类)
multiclass:多分类 softmax(分类)
multiclassova:多分类 one vs all(分类)
lambdarank:排序(排序)
…… | ㅤ |
根据场景确定 | num_class | 多分类问题的类别个数 | ㅤ | ㅤ | ㅤ | ㅤ | ㅤ |
根据场景确定 | boosting_type | 梯度提升决策树的类型 | 不同的boosting_type对应着不同的算法和策略。 | gbdt | str | gbdt:使用传统的梯度提升决策树算法,其中每棵树都是通过最小化损失函数的梯度来逐步拟合目标值(回归问题)或类别概率(分类问题)。
dart:在传统的梯度提升决策树算法的基础上引入了随机性和Dropout技术。DART在每次迭代中随机选择一部分树来训练,以减少过拟合的风险,并通过Dropout来减少树的复杂性。
rf:使用随机森林来训练模型。在每次迭代中,rf随机选择一部分特征子集和样本子集,然后基于这些子集构建一棵决策树。最后,通过多个随机森林模型的平均预测来进行预测。 | gbdt适用于各种问题,且在大多数情况下都能提供良好的性能。一般情况推荐默认值
DART在处理大规模数据集时特别有效。
rf适用于高维数据和噪声较多的情况。 |
搜索调参 | learning_rate / eta | 学习率 | 控制每次迭代中模型权重更新的步长或速度 | 0.1 | float | 0~1 | [0.01, 0.015, 0.025, 0.05, 0.1]
较大的学习率需要较小的迭代次数,而较小的学习率需要较大的迭代次数。 |
搜索调参 | n_estimators | 迭代次数 | 与学习率一起决定学习效率 | 100 | int | >0 | 配合
early_stopping:多少步没有提升就停止(fit 函数内)
eval_set :验证数据集(fit 函数内)
metric:评估指标
参数使用,如果没有提升则提前结束
在调参时有坑,慎用。提前结束是看模型在验证数据上的标签然后提前停止,但是验证数据的量相较于新数据集一般很小,所以提前结束的参数不适用。 |
搜索调参 | max_depth | 树的最大深度 | 控制决策树的复杂度和拟合能力,太大的值容易过拟合,太小容易欠拟合 | -1(不做限制) | ㅤ | ㅤ | 粗糙的根据数据量来大致尝试:
万级数据量:3~7
十万级数据:5~15
百万级或更多:10~20 |
搜索调参 | num_leaves | 每棵树的叶子节点的最大数量 | 控制决策树的复杂度和拟合能力,太大的值容易过拟合,太小榕溪欠拟合 | 31 | ㅤ | 应该小于 | |
根据场景确定 | is_unbalance / unbalanced_sets
class_weight(多分类) | 是否平衡样本 | ㅤ | false | bool | class_weight:dict, 'balanced' or None, optional (default=None) | ㅤ |
根据场景确定 | metric | 评估指标 | ㅤ | {l2 for regression}, {binary_logloss for binary classification}, {ndcg for lambdarank} | str or list | 回归任务:mae、mse、rmse
二分类:auc、average_precision、binary_logloss、binary_error
多分类:multiclass、multi_logloss、multi_error | ㅤ |
搜索调参 | min_data_in_leaf / min_child_samples | 叶子节点数据的最小数量 | ㅤ | 20 | ㅤ | ㅤ | 较大的min_data_in_leaf值会限制每个叶子节点上的样本数量,从而控制了模型的复杂度(防止过拟合)、提高模型的泛化能力(减少异常值影响 更稳定)、提高模型的运行速度。
如果数据集较小或特征较少,较小的值可能更适合 |
ㅤ | min_sum_hessian_in_leaf / min_child_weight | 指定孩子节点中最小的样本权重和 | ㅤ | 1e-3 | ㅤ | ㅤ | [1, 3, 5, 7],如果一个叶子节点的样本权重和小于min_child_weight则拆分过程结束 |
搜索调参 | colsample_bytree / feature_fraction | 特征随机采样的比例 | ㅤ | 1 | ㅤ | ㅤ | [0.6, 0.7, 0.8, 0.9, 1] |
搜索调参 | subsample / bagging_fraction | 样本随机采样的比例 | ㅤ | 1 | ㅤ | bagging_freq 设置为非0值时才生效 | [0.6, 0.7, 0.8, 0.9, 1] |
ㅤ | bagging_freq / subsample_freq | 禁用样本采样 | ㅤ | 0 | ㅤ | ㅤ | ㅤ |
搜索调参 | lambda_l1 / reg_alpha | ㅤ | ㅤ | 0 | ㅤ | ㅤ | 如果数据集非常大,特征数量很多,可以考虑使用较小的 lambda_l1 值,以控制模型的复杂度。
如果数据集相对较小,特征数量有限,可以尝试较大的 lambda_l1 值,以提高模型的泛化能力。 |
搜索调参 | lambda_l2 / reg_lambda | L2正则化权重项 | ㅤ | 0 | ㅤ | ㅤ | [0, 0.1, 0.5, 1],增加此值将使模型更加保守。 |
ㅤ | max_bin | 特征值将被归入的最大仓位数 | ㅤ | 255 | int | max_bin > 1 | LightGBM会根据max_bin自动压缩内存,数值越大越耗时 |
ㅤ | min_gain_to_split / min_split_gain | 执行切分的最小增益 | ㅤ | 0 | ㅤ | ㅤ | [0, 0.05 ~ 0.1, 0.3, 0.5, 0.7, 0.9, 1],设置的值越大,模型就越保守 |
ㅤ | seed / random_state | 随机数种子 | ㅤ | ㅤ | ㅤ | ㅤ | ㅤ |
ㅤ | verbose / verbosity | 控制日志的详细程度 | ㅤ | 1 | int | -1:完全不输出训练过程中的日志信息(静默模式)。
0:显示致命错误信息。
1:显示错误信息。
2:显示警告信息。
>2:显示详细信息(包括每一轮的日志)。 | 放在fit()方法中才会生效,不直接使用该参数
clf_lgbm.fit(train_X, train_y, callbacks=[lgbm.log_evaluation(1)]) |
1.5.3、调参实例
一般来说,开始选择一个较小的步长来网格搜索最好的迭代次数。
clf_lgbm = lgbm.LGBMClassifier( boosting_type='gbdt', # 第一步 根据场景固定部分参数 objective='binary', metric='auc', verbose=-1, learning_rate=0.1, # 第二步 学习率和迭代次数一起调 0.666700429456532 n_estimators=200, max_depth=5, # 第三步调 {max_depth,num_leaves}, 0.6708004303847365 num_leaves=20, min_data_in_leaf=50, # 第四步调 min_data_in_leaf, 0.6728529685838128 bagging_fraction=0.7, # 第五步调 {bagging_fraction,feature_fraction}, 0.6728529685838128 feature_fraction=1, # lambda_l1=1, # 第六步调 {lambda_l1,lambda_l2}, 0.6714313656366919 # lambda_l2=1, # learning_rate=0.1, # 第七步调, learning_rate, 最佳0.1, 0.6714313656366919 ) param_grid = { # 'n_estimators': range(100,501 ,100), # 'max_depth': range(1, 6, 1), # 'num_leaves':range(15, 36, 5), # 'min_data_in_leaf': range(20, 80, 10), # 'feature_fraction': [0.7,0.8,0.9,1.0], # 'bagging_fraction': [0.7,0.8,0.9,1.0], 'lambda_l1': [1e-5,1e-1,0.0,0.1,0.5,1.0], 'lambda_l2': [1e-5,1e-1,0.0,0.1,0.5,1.0], # 'learning_rate': [0.01, 0.015, 0.025, 0.05, 0.1] } gs_lgbm = GridSearchCV(clf_lgbm, param_grid=param_grid, scoring='roc_auc') gs_lgbm.fit(train_data_array, train_label) print('最优参数组合:',gs_lgbm.best_params_) print('最优参数分数:',gs_lgbm.best_score_) # print(gs_lgbm.scorer_)
1.5.4、特征重要性
boost = clf_lgbm.booster_ pd.DataFrame({ 'column': train_data_value_all_df.columns, 'importance': boost.feature_importance(), }).sort_values(by='importance')
1.5.5、参考文档
稀疏矩阵分类
稀疏矩阵的特点是特征数量可能非常巨大,通常几万几十万。这个时候如果继续选择普通的分类模型,由于普通模型可能会对特征进行遍历,就会导致分类器的运行效率极其低下。此时就需要选择合适的分类器来执行任务。
稀疏矩阵常用的分类器有:
名称 | 分类器 | 输出类型 | 备注 |
逻辑回归 | LogisticRegression | 软预测 | ㅤ |
线性支持向量机 | LinearSVC | 硬预测 | 只能输出类别,不能输出概率 |
随机梯度下降分类器 | SGDClassifier | 软预测 | ㅤ |
被动-侵略性分类器 | PassiveAggressiveClassifier | 硬预测 | 只能输出类别,不能输出概率 |
先验为伯努利分布的朴素贝叶斯 | BernoulliNB | 软预测 | 样本特征是二元离散值或者很稀疏的多元离散值 |
先验为多项式分布的朴素贝叶斯 | MultinomialNB | 软预测 | 样本特征的分大部分是多元离散值 |
1.6、集成学习分类器 VotingClassifier
通过结合多个独立的分类器(或回归器)的预测结果来进行预测
sklearn.ensemble.VotingClassifier(estimators, voting='hard', weights=None, n_jobs=None, flatten_transform=True)
参数说明:
estimators:一个列表或字典,其中包含要结合的分类器。列表的每个元素都是一个元组,包含一个分类器的名称(字符串)和一个分类器对象。字典的键是分类器的名称,值是分类器对象。
voting:指定投票策略的字符串。可以是以下三个值之一:'hard':选取预测结果中的多数类别作为最终预测结果。'soft':对预测结果进行加权平均,然后根据平均值确定最终的预测结果。'uniform':对预测结果进行加权平均,并对所有权重进行归一化。
weights:一个列表或字典,包含每个分类器的权重。列表的长度必须与estimators中的分类器数量相同。如果未指定权重,则所有分类器的权重默认相等。
n_jobs:并行运行分类器的数量。默认为None,表示不并行运行。
flatten_transform:指定是否将输入数据展平为二维数组。默认为True,表示将输入数据展平。
属性和方法:
estimators_:一个字典,包含所有分类器的名称和对象。
classes_:一个数组,包含训练数据中的所有类别。
named_estimators_:一个字典,包含所有分类器的名称和对象。
fit(X, y):使用训练数据X和标签y来拟合集成分类器。
predict(X):对输入数据X进行预测。
predict_proba(X):对输入数据X返回每个类别的概率。
score(X, y):计算使用输入数据X和标签y的分类器的准确率。
基分类器的数量权衡
数量不一定越多越好,增加基分类器的数量可能会增加模型的复杂度和计算开销,但并不总是会带来性能的提升。
- 数据集的规模:如果数据集较小,增加基分类器的数量可能会增加过拟合的风险。在这种情况下,选择较少的基分类器可能更合适。
- 基分类器之间的差异性:基分类器之间的差异性越大,集成学习的效果可能会更好。因此,如果有多个不同类型的强分类器可用,可以考虑增加基分类器的数量。
- 计算资源:增加基分类器的数量会增加计算资源的需求。如果计算资源有限,可能需要权衡基分类器的数量和计算开销之间的平衡。
- 集成学习的目标:根据具体的集成学习目标,选择合适的基分类器数量。有时候,使用较少的基分类器就能达到预期的性能。
二、聚类算法
# 划分聚类 from sklearn.cluster import KMeans # KMeans聚类 from sklearn.cluster import MiniBatchKMeans # KMeans聚类大样本优化 # 层次聚类 from sklearn.cluster import Birch # 密度聚类 from sklearn.cluster import DBSCAN from sklearn.cluster import OPTICS # 谱聚类 from sklearn.cluster import SpectralClustering
不严谨对比
聚类算法 | 运行效率 | 适合数据 |
KMeans | O(n * K * I * d)
n是数据量
K簇的数量
I是迭代次数
d是数据维度 | 非凸数据效果不佳
对于噪声敏感
需指定簇的数量 |
MiniBatchKMeans | O(n * K * I * d) | 由于使用小批量数据,计算速度更快。
适用于大规模数据集,对于较大的K和高维数据表现较好。 |
Birch | O(n) | 非凸数据效果不佳
适用于大规模数据集
适合类别数比较多的数据集
对噪声不敏感
不适合特征维数较高的数据集 |
DBSCAN | O(n * log(n)) | 适用于各种密度和不规则形状的数据集,
不需要提前指定簇的数量。
对噪声不敏感 |
OPTICS | O(n * log(n)) | 可以在不指定密度阈值的情况下自适应地发现簇。 |
SpectralClustering | O(n^3) | 稀疏数据、适用于小到中等规模的数据集 |
2.1、KMeans聚类
2.1.1、概述
计算样本点与类簇质心的距离,与类簇质心相近的样本点划分为同一类簇。k‐均值通过样本间的距离来衡量它们之间的相似度,两个样本距离越远,则相似度越低,否则相似度越高。
算法流程:
- 选择 K 个初始质心(K需要用户指定),初始质心随机选择即可,每一个质心为一个类
- 对剩余的每个样本点,计算它们到各个质心的欧式距离,并将其归入到相互间距离最小的质心所在的簇。计算各个新簇的质心。
- 在所有样本点都划分完毕后,根据划分情况重新计算各个簇的质心所在位置,然后迭代计算各个样本点到各簇质心的距离,对所有样本点重新进行划分
- 重复2. 和 3.,直到质心不在发生变化时或者到达最大迭代次数时
优点:
- 原理简单,容易实现,且运行效率比较高
- 结果容易解释,适用于高维数据的聚类
缺点:
- K值的选取不好把握
- 采用贪心策略,导致容易局部收敛,在大规模数据集上求解较慢
- 对离群点和噪声点非常敏感,少量的离群点和噪声点可能对算法求平均值产生极大影响,从而影响聚类结果
- 初始聚类中心的选取也对算法结果影响很大,不同的初始中心可能会导致不同的聚类结果
2.1.2、示例&调参
from sklearn.cluster import KMeans from sklearn import datasets iris = datasets.load_iris() # 加载数据 X = iris.data y = iris.target est = KMeans(n_clusters=3) # 定义模型 y_pred = est.fit_predict(X) # 聚类 """ array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1, 1, 2, 2, 2, 2, 1, 2, 1, 2, 1, 2, 2, 1, 1, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 2, 1, 2, 2, 1], dtype=int32) """
2.1.3、参数详解(部分)
参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
n_clusters | k值,聚几类 | 8 | int | ㅤ | ㅤ |
max_iter | 最大的迭代次数 | 300 | int | ㅤ | 一般如果是凸数据集的话可以不管这个值,如果数据集不是凸的,可能很难收敛,此时可以指定最大的迭代次数让算法可以及时退出循环。 |
n_init | 用不同的初始化质心运行算法的次数 | 10 | ‘auto’ or int | ㅤ | 由于K-Means是结果受初始值影响的局部最优的迭代算法,因此需要多跑几次以选择一个较好的聚类效果,一般不需要改。如果你的k值较大,则可以适当增大这个值。 |
init | 初始值选择的方式 | k-means++ | ㅤ | k-means++(初始化优化)
random
自定义初始化的k个质心 | 一般建议使用默认的'k-means++'。 |
algorithm | 算法选择 | lloyd | ㅤ | “lloyd”:
“elkan”:elkan K-Means算法(距离计算优化)
“auto”:弃用
“full”:弃用 | 一般数据是稠密的,那么就是 “elkan”,否则就是"lloyd"。一般来说建议直接用默认的"lloyd” |
K值的选取:
通过评估聚类的结果来选择K值,聚类结果的评估通常有轮廓系数(Silhouette Coefficient)和CH(Calinski-Harabasz Index)。详见 2.5、聚类模型评估
2.1.4、大样本优化Mini Batch K-Means
在统的K-Means算法中,要计算所有的样本点到所有的质心的距离。如果样本量非常大,比如达到10万以上,特征有100以上,此时用传统的K-Means算法非常的耗时,就算加上elkan K-Means优化也依旧。在大数据时代,这样的场景越来越多。此时Mini Batch K-Means应运而生。顾名思义,Mini Batch,也就是用样本集中的一部分的样本来做传统的K-Means,这样可以避免样本量太大时的计算难题,算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。
在Mini Batch K-Means中,我们会选择一个合适的批样本大小batch size,我们仅仅用batch size个样本来做K-Means聚类。那么这batch size个样本怎么来的?一般是通过无放回的随机采样得到的。为了增加算法的准确性,我们一般会多跑几次Mini Batch K-Means算法,用得到不同的随机采样集来得到聚类簇,选择其中最优的聚类簇。也可以使用MiniBatchKMeans的增量学习进行训练
示例&调参
from sklearn.cluster import MiniBatchKMeans import numpy as np X = np.array([[1, 2], [1, 4], [1, 0], [4, 2], [4, 0], [4, 4], [4, 5], [0, 1], [2, 2], [3, 2], [5, 5], [1, -1]]) # manually fit on batches kmeans = MiniBatchKMeans(n_clusters=2, random_state=0, batch_size=6, n_init="auto") kmeans = kmeans.partial_fit(X[0:6,:]) # 增量学习 kmeans = kmeans.partial_fit(X[6:12,:]) # 增量学习 print(kmeans.cluster_centers_) # 打印聚类中心,每个聚类中心是一个二维坐标 kmeans.predict([[0, 0], [4, 4]]) # 聚类预测
参数详解
参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
n_clusters | k值,聚几类 | 8 | int | ㅤ | ㅤ |
batch_size | 用来跑Mini Batch KMeans算法的采样集的大小 | 1024 | int | ㅤ | ㅤ |
init | 初始值选择的方式 | k-means++ | ㅤ | k-means++(初始化优化)
random
自定义初始化的k个质心 | 一般建议使用默认的'k-means++'。 |
n_init | 用不同的初始化质心运行算法的次数 | 3 | ‘auto’ or int | ㅤ | 由于K-Means是结果受初始值影响的局部最优的迭代算法,因此需要多跑几次以选择一个较好的聚类效果,一般不需要改。如果你的k值较大,则可以适当增大这个值。 |
max_iter | 最大的迭代次数 | 100 | int | ㅤ | 一般如果是凸数据集的话可以不管这个值,如果数据集不是凸的,可能很难收敛,此时可以指定最大的迭代次数让算法可以及时退出循环。 |
reassignment_ratio | 某个类别质心被重新赋值的最大次数比例 | 0.01 | float | ㅤ | 这个比例是占样本总数的比例,乘以样本总数就得到了每个类别质心可以重新赋值的次数。如果取值较高的话算法收敛时间可能会增加,尤其是那些暂时拥有样本数较少的质心。默认是0.01。如果数据量不是超大的话,比如1w以下,建议使用默认值。如果数据量超过1w,类别又比较多,可能需要适当减少这个比例值。具体要根据训练集来决定。 |
max_no_improvement | 连续多少个Mini Batch没有改善聚类效果的话,就停止算法 | 10 | int | ㅤ | ㅤ |
2.1.5、参考文章
2.2、BIRCH聚类
2.2.1、概述
层次聚类
层次聚类算法可以揭示数据的分层结构,在树形结构上不同层次进行划分,可以得到不同粒度的聚类结果。按照层次聚类的过程分为自底向上的聚合聚类和自顶向下的分裂聚类。聚合聚类以AGNES、BIRCH、ROCK等算法为代表,分裂聚类以DIANA算法为代表。
- 自底向上的聚合聚类将每个样本看作一个簇,初始状态下簇的数目等于样本的数目,然后然后根据一定的算法规则,例如把簇间距离最小的相似簇合并成越来越大的簇,直到满足算法的终止条件。
- 自顶向下的分裂聚类先将所有样本看作属于同一个簇,然后逐渐分裂成更小的簇,直到满足算法终止条件为止。
BIRCH的全称是利用层次方法的平衡迭代规约和聚类(Balanced Iterative Reducing and Clustering Using Hierarchies)
优点:
- 节约内存,所有的样本都在磁盘上,CF Tree仅仅存了CF节点和对应的指针。
- 聚类速度快,只需要一遍扫描训练集就可以建立CF Tree,CF Tree的增删改都很快。
- 可以识别噪音点,还可以对数据集进行初步分类的预处理
缺点:
- 由于CF Tree对每个节点的CF个数有限制,导致聚类的结果可能和真实的类别分布不同.
- 对高维特征的数据聚类效果不好。此时可以选择Mini Batch K-Means
- 如果数据集的分布簇不是类似于超球体,或者说不是凸的,则聚类效果不好。
2.2.2、示例&调参
from sklearn.cluster import Birch X = [[0, 1], [0.3, 1], [-0.3, 1], [0, -1], [0.3, -1], [-0.3, -1]] brc = Birch(n_clusters=None) brc.fit(X) brc.predict(X)
2.2.3、参数详解
参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
threshold | 叶节点每个CF的最大样本半径阈值T | 0.5 | float | 0到正无穷 | 一般来说threshold越小,则CF Tree的建立阶段的规模会越大,即BIRCH算法第一阶段所花的时间和内存会越多。 |
branching_factor | CF Tree内部节点的最大CF数B,以及叶子节点的最大CF数L | 50 | int | ㅤ | 如果样本量非常大,比如大于10万,则一般需要增大这个默认值。选择多大的branching_factor以达到聚类效果则需要通过和threshold一起调参决定 |
n_clusters | 类别数K | 3 | None,int | ㅤ | 不输入K,则BIRCH会对CF Tree里各叶子节点CF中样本的情况自己决定类别数K值,如果输入K值,则BIRCH会CF Tree里各叶子节点CF进行合并,直到类别数为K。 |
compute_labels | 是否标示类别输出 | True | bool | ㅤ | ㅤ |
2.2.4、参考文章:
2.3、DBSCAN聚类
2.3.1、概述
DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪声的基于密度的聚类方法)是一种很典型的密度聚类算法
该算法将具有足够密度的区域划分为簇,并在具有噪声的空间数据库中发现任意形状的簇,它将簇定义为密度相连的点的最大集合。
和传统的K-Means算法相比,DBSCAN最大的不同就是不需要输入类别数k,当然它最大的优势是可以发现任意形状的聚类簇,而不是像K-Means,一般仅仅使用于凸的样本集聚类。同时它在聚类的同时还可以找出异常点,这点和BIRCH算法类似。那么我们什么时候需要用DBSCAN来聚类呢?一般来说,如果数据集是稠密的,并且数据集不是凸的,那么用DBSCAN会比K-Means聚类效果好很多。如果数据集不是稠密的,则不推荐用DBSCAN来聚类。
优点:
1) 可以对任意形状的稠密数据集进行聚类,相对的,K-Means之类的聚类算法一般只适用于凸数据集。
2) 可以在聚类的同时发现异常点,对数据集中的异常点不敏感。
3) 聚类结果没有偏倚,相对的,K-Means之类的聚类算法初始值对聚类结果有很大影响。
缺点:
1)如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差,这时用DBSCAN聚类一般不适合。
2) 如果样本集较大时,聚类收敛时间较长,此时可以对搜索最近邻时建立的KD树或者球树进行规模限制来改进。
3) 调参相对于传统的K-Means之类的聚类算法稍复杂,主要需要对距离阈值ϵ,邻域样本数阈值MinPts联合调参,不同的参数组合对最后的聚类效果有较大影响。
2.3.2、示例&调参
from sklearn.cluster import DBSCAN y_pred = DBSCAN(eps=0.1, min_samples=10).fit_predict(X)
eps和min_samples需要进行联合调参;
有时候所有的样本都会被预测为-1,则可能是参数不对,所有的数据都能被预测为了噪音
2.3.3、参数详解
参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
eps | ϵ-邻域的距离l阈值 | 0.5 | float | ㅤ | eps过大,则更多的点会落在核心对象的ϵ-邻域,此时我们的类别数可能会减少, 本来不应该是一类的样本也会被划为一类。反之则类别数可能会增大,本来是一类的样本却被划分开。 |
min_samples | 邻域最小样本数 | 5 | int | ㅤ | 在eps一定的情况下,min_samples过大,则核心对象会过少,此时簇内部分本来是一类的样本可能会被标为噪音点,类别数也会变多。反之min_samples过小的话,则会产生大量的核心对象,可能会导致类别数过少。通常设置为特征维度+1 |
metric | 最近邻距离度量参数 | euclidean | ㅤ | euclidean:欧式距离
manhattan:曼哈顿距离
chebyshev:切比雪夫距离
minkowski:闵可夫斯基距离 | 推荐默认 |
2.3.4、OPTICS聚类
详见:OPTICS聚类
2.3.5、参考文章
2.4、谱聚类
2.4.1、概述
谱聚类是从图论中演化出来的算法,后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点,这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。
刘建平大佬的建议:在处理实际的聚类问题时,个人认为谱聚类是应该首先考虑的几种算法之一。
优点:
1)谱聚类只需要数据之间的相似度矩阵,因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
2)由于使用了降维,因此在处理高维数据聚类时的复杂度比传统聚类算法好。
缺点:
1)如果最终聚类的维度非常高,则由于降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好。
2) 聚类效果依赖于相似矩阵,不同的相似矩阵得到的最终聚类效果可能很不同。
2.4.2、示例&调参
import numpy as np from sklearn import datasets X, y = datasets.make_blobs(n_samples=500, n_features=6, centers=5, cluster_std=[0.4, 0.3, 0.4, 0.3, 0.4], random_state=11) from sklearn.cluster import SpectralClustering y_pred = SpectralClustering().fit_predict(X) from sklearn import metrics print("Calinski-Harabasz Score", metrics.calinski_harabasz_score(X, y_pred)) for index, gamma in enumerate((0.01,0.1,1,10)): for index, k in enumerate((3,4,5,6)): y_pred = SpectralClustering(n_clusters=k, gamma=gamma).fit_predict(X) print("Calinski-Harabasz Score with gamma=", gamma, "n_clusters=", k,"score:", metrics.calinski_harabasz_score(X, y_pred))
需要对k和gamma进行联合调参
2.4.3、参数详解
参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
n_clusters | 谱聚类切图时降维到的维数
也是最后聚类的类别数 | 8 | int | ㅤ | 可选的,但是一般还是推荐调参选择最优参数。 |
affinity | 相似矩阵的建立方式 | rbf | str or callable | ㅤ | 推荐使用默认的高斯核函数。是用高斯核函数需要对gamma进行调参 |
gamma | 核函数参数 | 1.0 | float | ㅤ | ㅤ |
2.4.4、参考文章
2.5、聚类模型评估
2.5.1、CH评估
CH(Calinski-Harabasz Index)指标通过计算类中各点与类中心的距离平方和来度量类内的紧密度,通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度,CH指标由分离度与紧密度的比值得到。从而,CH越大代表着类自身越紧密,类与类之间越分散,即更优的聚类结果。
效率问题:不需要考虑样本之间的距离计算,而是仅仅涉及聚类中心之间的距离计算,在数据量较大时相较于轮廓系数更快
from sklearn import metrics metrics.calinski_harabaz_score(X, y_pred)
2.5.2、轮廓系数
轮廓系数(Silhouette Coefficient)取值范围为[-1,1],取值越接近1则说明聚类性能越好,相反,取值越接近-1则说明聚类性能越差。
效率问题:因为轮廓系数需要计算每个样本与其所属聚类之外的其他聚类的距离,涉及到大量的距离计算,所以数据量大时非常耗时
from sklearn import metrics metrics.silhouette_samples(X, y_pred, metric='euclidean') """ metric : 计算要素阵列中实例之间的距离时使用的度量。默认是euclidean(欧氏距离)。 如果metric是字符串,则必须是允许的选项之一metrics.pairwise.pairwise_distances。如果X是距离数组本身,请使用metric="precomputed"。 """
三、降维算法
from sklearn.decomposition import PCA from sklearn.decomposition import KernelPCA from sklearn.decomposition import IncrementalPCA from sklearn.decomposition import SparsePCA from sklearn.decomposition import MiniBatchSparsePCA from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.manifold import LocallyLinearEmbedding from sklearn.manifold import TSNE
算法 | 适用场景 |
PCA | 传统机器学习场景 |
LDA | 带标签数据
图形图像识别领域 |
LLE | 高维数据可视化
图形图像识别领域 |
TSNE | 高维数据可视化 |
3.1、PCA主成分分析
3.1.1、概述
PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。数据维度降低,信息肯定会有损失,但是我们希望损失尽可能的小。假设存在一个线性的超平面,可以让我们对数据进行投影。降维的标准为:样本点到这个超平面的距离足够近,或者说样本点在这个超平面上的投影能尽可能的分开。
算法流程:


优点:
- 仅仅需要以方差衡量信息量,不受数据集以外的因素影响。
- 各主成分之间正交,可消除原始数据成分间的相互影响的因素。
- 计算方法简单,主要运算是特征值分解,易于实现。
缺点:
- 主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。
- 方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。
3.1.2、示例
创建数据
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits import mplot3d %matplotlib inline from sklearn.datasets import make_blobs # X为样本特征,Y为样本簇类别, 共1000个样本,每个样本3个特征,共4个簇 X, y = make_blobs(n_samples=10000, n_features=3, centers=[[3,3, 3], [0,0,0], [1,1,1], [2,2,2]], cluster_std=[0.2, 0.1, 0.2, 0.2], random_state =9) fig = plt.figure() ax = plt.axes(projection='3d') ax.scatter(X[:, 0], X[:, 1], X[:, 2],marker='o')
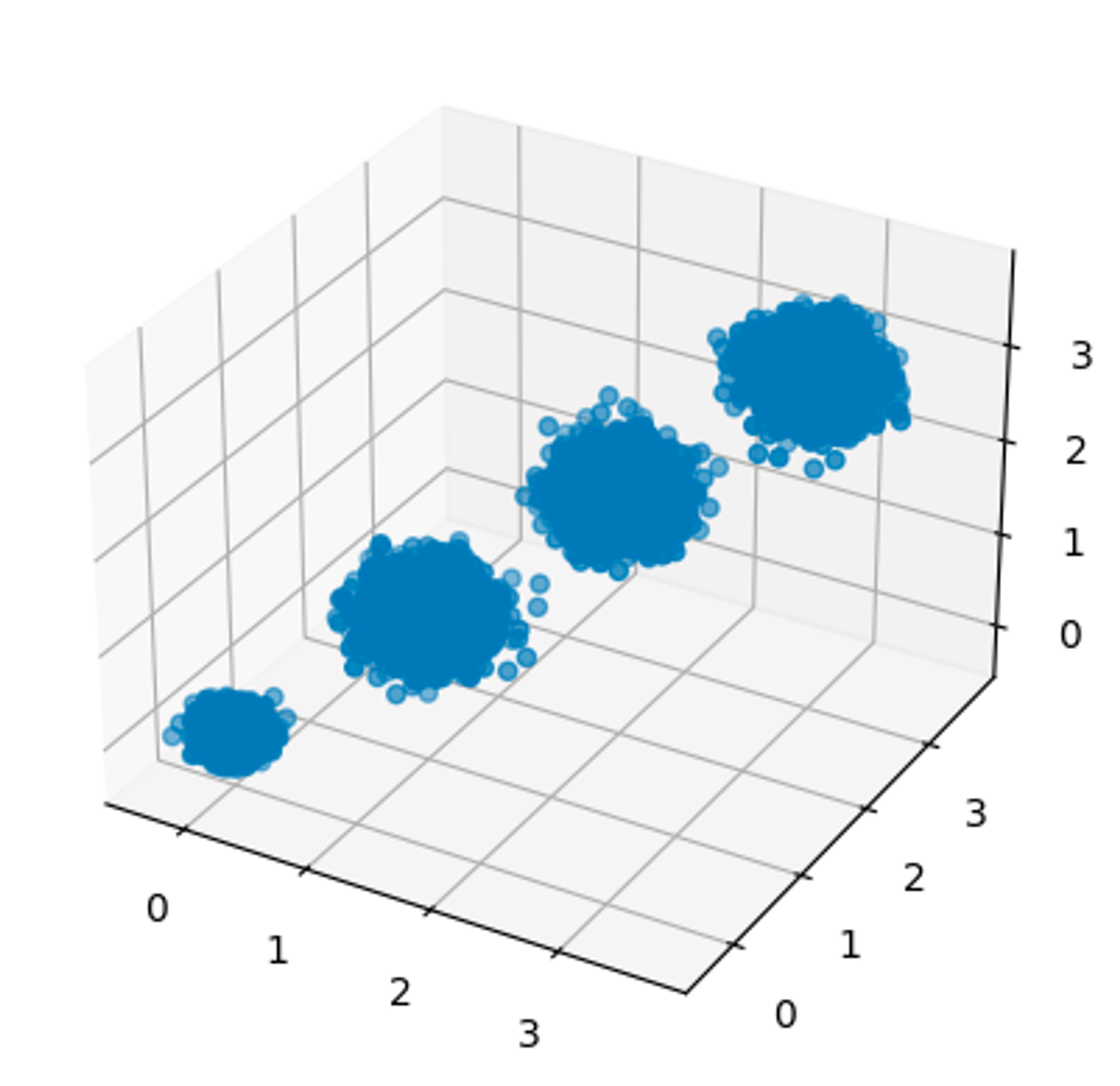
from sklearn.decomposition import PCA pca = PCA(n_components=3) # 数据本来就是三维,如果降维后的维度也设置为3,则是单纯的对数据投影,可以通过此方法查看特征方差分布 pca.fit(X) print(pca.explained_variance_ratio_) # 各特征的方差值占比 print(pca.explained_variance_) # 各特征的方差值 """ [0.98318212 0.00850037 0.00831751] [3.78521638 0.03272613 0.03202212] """
3.1.3、参数
pac最主要的参数就是
n_components,该参数的含义是要保存的特征数量或方差占比总和3.1.4、PCA对比
PCA种类 | 区别 | API | 调参 |
PCA | 线性数据的降维 | from sklearn.decomposition import PCA | ㅤ |
KernelPCA | 非线性数据的降维,需要用到核技巧 | from sklearn.decomposition import KernelPCA | 核函数的参数进行调参 |
IncrementalPCA | 解决单机内存限制,将数据分成多个batch,然后对每个batch依次递增调用partial_fit函数 | from sklearn.decomposition import IncrementalPCA | n_components只能是整数 |
SparsePCA | 使用L1正则化,将非主要成分的影响度降为0,只需要对主要的成分进行PCA降维,避免噪声影响 | from sklearn.decomposition import SparsePCA | 对L1正则化参数进行调参 |
MiniBatchSparsePCA | 使用L1正则化,
通过使用一部分样本特征和给定的迭代次数来进行PCA降维,以解决在大样本时特征分解过慢的问题,代价就是PCA降维的精确度可能会降低 | from sklearn.decomposition import MiniBatchSparsePCA | 对L1正则化参数进行调参 |
3.2、LDA线性判别
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。
LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。
LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向。
LDA降维最多降到类别数k-1的维数,而PCA没有这个限制。
LDA在模式识别领域(比如人脸识别,舰艇识别等图形图像识别领域)中有非常广泛的应用
import numpy as np from sklearn.discriminant_analysis import LinearDiscriminantAnalysis X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]]) y = np.array([1, 1, 1, 2, 2, 2]) lda = LinearDiscriminantAnalysis(n_components=1) lda.fit(X, y) X_new = lda.transform(X)
参数 | 含义 | 默认值 | 类型 | 可选项 | 选择经验 |
n_components | 降维后的维度 | None | int | [1,类别数-1) | 如果不是用于降维,则这个值可以用默认的None。 |
solver | 求LDA超平面特征矩阵使用的方法 | svd | str | 奇异值分解"svd"
最小二乘"lsqr"
特征分解"eigen” | "eigen"。一般来说特征数非常多的时候推荐使用svd,而特征数不多的时候推荐使用eigen |
priors | 类别权重 | None | array-like of shape (n_classes,) | ㅤ | 降维时一般不需要关注这个参数 |
shrinkage | 正则化参数 | None | ‘auto’ or float, | ㅤ | 降维时一般不需要关注这个参数 |
一般来说,如果我们的数据是有类别标签的,那么优先选择LDA去尝试降维;当然也可以使用PCA做很小幅度的降维去消去噪声,然后再使用LDA降维。如果没有类别标签,那么肯定PCA是最先考虑的一个选择了。
3.3、LLE局部线性嵌入
由于LLE在降维时保持了样本的局部特征,它广泛的用于图像图像识别,高维数据可视化等领域。
LLE是广泛使用的图形图像降维方法,它实现简单,但是对数据的流形分布特征有严格的要求。比如不能是闭合流形,不能是稀疏的数据集,不能是分布不均匀的数据集等等。所以不常用
from sklearn.datasets import load_digits from sklearn.manifold import LocallyLinearEmbedding X, _ = load_digits(return_X_y=True) X.shape embedding = LocallyLinearEmbedding(n_components=2) X_transformed = embedding.fit_transform(X[:100]) X_transformed.shape
3.4、tSNE T分布随机近邻嵌入
tSNE是一种降维技术,即将多维数据非线性的转换为低纬数据。形式上和PCA很像,根本差异在于PCA主要用于数据处理,即PCA在实现数据降维的同时,也实现了噪音去除;而tSNE主要用于数据展示,即将不能可视化的多维数据降维到低维(如2维),进行数据可视化展示。另外PCA是线性的,可对新的test数据进行同样的降维处理,而tSNE是非线性的,不能对新的test数据进行同样的降维处理。
import numpy as np from sklearn.manifold import TSNE X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]]) X_embedded = TSNE(n_components=2, learning_rate='auto', init='random', perplexity=3).fit_transform(X) X_embedded.shape
四、关联规则算法
4.1、Apriori
Apriori 算法是常用的用于挖掘出数据关联规则的算法,它用来找出数据值中频繁出现的数据集合,找出这些集合的模式有助于我们做一些决策。
但是scikit-learn中并没有频繁集挖掘相关的算法类库,常用的关联规则算法库为
mlxtend和efficient-apriori库 ,但是这两个库都只有apriori算法的实现 。详见Apriori 4.2、FP Tree
Apriori算法需要多次扫描数据,I/O是很大的瓶颈。为了解决这个问题,FP Tree算法(也称FP Growth算法)采用了一些技巧,无论多少数据,只需要扫描两次数据集,因此提高了算法运行的效率。
4.3、PrefixSpan
序列数据的频繁项集挖掘。
比如第一个序列<a(abc)(ac)d(cf)>,它由a,abc,ac,d,cf共5个项集数据组成,并且这些项有时间上的先后关系。对于多于一个项的项集我们要加上括号,以便和其他的项集分开。同时由于项集内部是不区分先后顺序的,为了方便数据处理,我们一般将序列数据内所有的项集内部按字母顺序排序。
自动化调参
超参数优化
GridSearchCV:网格搜索
from sklearn.model_selection import GridSearchCV """ GridSearchCV(estimator, param_grid, *, scoring=None, n_jobs=None, refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', error_score=nan, return_train_score=False) - estimator:所使用的分类器 - param_grid:值为字典或者列表,即需要最优化的参数的取值 - scoring:准确度评价标准,默认None. - 常用评分标准设置:‘accuracy’、‘precision’、‘recall’、‘f1’、‘roc_auc’ - scoring 设置参考: - https://blog.csdn.net/qq_41076797/article/details/102755893 - https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter - n_jobs:并行数,int,默认1,-1表示使用所有能用的核 - cv:交叉验证次数,int,默认5, """ from sklearn import svm, datasets from sklearn.model_selection import GridSearchCV iris = datasets.load_iris() parameters = {'kernel':('linear', 'rbf'), 'C':[1, 10]} svc = svm.SVC() grid_search = GridSearchCV(svc, parameters) grid_search.fit(iris.data, iris.target) grid_search.best_score_ # 获取最高分 grid_search.best_params_ # 获取被搜索的最好参数 grid_search.best_estimator_ # 获取最佳估计器(带所有参数的值)
RandomizedSearchCV:随机网格搜索
from sklearn.model_selection import RandomizedSearchCV from sklearn.ensemble import RandomForestClassifier from scipy.stats import randint from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split # 加载数据 X, y = load_iris(return_X_y=True) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) model = RandomForestClassifier() param_dist = { 'n_estimators': randint(50, 200), # 树的数量 'max_features': ['auto', 'sqrt', 'log2'], # 特征选择策略 'max_depth': randint(1, 20), # 树的最大深度 'min_samples_split': randint(2, 10) # 内部节点再划分所需的最小样本数 } random_search = RandomizedSearchCV(model, param_distributions=param_dist, n_iter=100, cv=5, verbose=1, random_state=42, n_jobs=-1) random_search.fit(X_train, y_train) print("Best parameters found: ", random_search.best_params_) print("Best score found: ", random_search.best_score_) best_model = random_search.best_estimator_ score = best_model.score(X_test, y_test) print("Test set score: ", score) """ RandomizedSearchCV( estimator=model, # 要优化的模型(估计器) param_distributions=param_dist, # 字典或列表,指定要调优的超参数及其分布。 scoring=roc_auc, # 评估指标,详见:https://scikit-learn.org/stable/modules/model_evaluation.html#scoring-parameter;设置多个评估指标:scoring = {'accuracy': 'accuracy', 'precision': 'precision', 'recall': 'recall', 'f1': 'f1'} n_iter=100, # 要随机选择的参数组合的数量。训练次数=min(超参数空间组合数, n_iter) cv=5, # 指定交叉验证的折数。 verbose=1, # 控制详细程度。0 表示不输出,1 表示输出简单信息,2 或更高则输出更详细的信息。 random_state=42, # 随机数生成器的种子,用于确保结果的可重现性。 n_jobs=-1, # 并行执行的作业数。-1 表示使用所有可用的 CPU 核心,1 表示单线程执行。 return_train_score=True # 如果设置为 True,将返回训练集的分数。默认值为 False。 ) """
from sklearn import datasets from sklearn.model_selection import RandomizedSearchCV from sklearn.svm import SVC from sklearn.model_selection import train_test_split from scipy.stats import uniform from sklearn.metrics import f1_score, make_scorer # 加载数据集 iris = datasets.load_iris() X = iris.data y = iris.target # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 定义模型 model = SVC() # 定义超参数空间 param_distributions = { 'C': uniform(0.1, 10), # 正则化参数 'kernel': ['linear', 'rbf'], # 核函数类型 'gamma': ['scale', 'auto'] + list(uniform(0.001, 0.1).rvs(10)), # 核系数 } # 定义自定义评分函数 f1_scorer = make_scorer(f1_score, average='weighted') # 定义随机搜索 random_search = RandomizedSearchCV( model, param_distributions=param_distributions, n_iter=50, # 采样次数 cv=5, # 交叉验证折数 scoring=f1_scorer, # 使用自定义评分函数 random_state=42, n_jobs=-1 # 使用所有CPU核心 ) # 执行随机搜索 random_search.fit(X_train, y_train) # 输出最佳参数 print("Best parameters found: ", random_search.best_params_) # 使用最佳参数的模型进行预测 best_model = random_search.best_estimator_ y_pred = best_model.predict(X_test) # 输出模型性能 from sklearn.metrics import accuracy_score print("Test accuracy: ", accuracy_score(y_test, y_pred)) print("Test F1 score: ", f1_score(y_test, y_pred, average='weighted'))
Bayesian Optimization:贝叶斯优化
贝叶斯优化(Bayesian Optimization)是一种用于全局优化的技术,特别适用于高维、非凸、昂贵的目标函数。在机器学习中,贝叶斯优化常用于超参数调优,因为它可以在较少的评估次数下找到接近最优的超参数配置。
他是通过拟合一个超参数到评估指标的一个函数,然后求最优解。
scikit-learn本身并没有内置的贝叶斯优化工具,但你可以使用第三方库如scikit-optimize(简称skopt)来实现贝叶斯优化。pip install scikit-optimizefrom sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.svm import SVC from sklearn.metrics import accuracy_score from skopt import BayesSearchCV from skopt.space import Real, Categorical, Integer # 加载数据集 iris = datasets.load_iris() X = iris.data y = iris.target # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 定义模型 model = SVC() # 定义超参数空间 param_space = { 'C': Real(0.1, 10, prior='log-uniform'), # 正则化参数 'kernel': Categorical(['linear', 'rbf']), # 核函数类型 'gamma': Real(0.001, 0.1, prior='log-uniform'), # 核系数 } # 定义贝叶斯搜索 bayes_search = BayesSearchCV( model, param_space, n_iter=50, # 采样次数 cv=5, # 交叉验证折数 random_state=42, n_jobs=-1 # 使用所有CPU核心 ) # 执行贝叶斯搜索 bayes_search.fit(X_train, y_train) # 输出最佳参数 print("Best parameters found: ", bayes_search.best_params_) # 使用最佳参数的模型进行预测 best_model = bayes_search.best_estimator_ y_pred = best_model.predict(X_test) # 输出模型性能 print("Test accuracy: ", accuracy_score(y_test, y_pred))
n_iter参数在贝叶斯优化中表示要进行的优化迭代次数,即在超参数空间中采样的次数。选择合适的n_iter值是一个权衡计算资源和优化效果的问题。以下是一些一般性的建议:1. 初始探索阶段
在初始探索阶段,通常建议设置较小的
n_iter值,以便快速了解超参数空间的大致情况。这个阶段的目的是识别出哪些超参数对模型性能影响较大。- 建议区间:10-50次迭代
2. 详细优化阶段
在初始探索阶段之后,可以根据初步结果调整超参数空间,并增加
n_iter值以进行更详细的优化。这个阶段的目的是找到更接近最优的超参数配置。- 建议区间:50-200次迭代
3. 计算资源允许的情况下
如果计算资源允许,可以进一步增加
n_iter值,以获得更精确的优化结果。通常,迭代次数越多,找到最优超参数配置的可能性越大,但计算成本也会相应增加。- 建议区间:200-500次迭代
Hyperband优化
Hyperband 是一种用于超参数优化的算法,特别适用于高维、昂贵的目标函数。它通过动态分配资源来加速超参数搜索过程。Hyperband 结合了随机搜索和早停策略,以在有限的计算资源下找到接近最优的超参数配置。
Hyperband的思想是跑多个Successive Halving
Successive Halving的思想如下:
- 假设优化算法关注n组参数,每组参数训练m轮;
- 在第一时刻n=16,m=25,进行训练;
- 第一时刻训练完成之后保留效果最好的前一半的参数,并加大训练轮数m
- 在第二时刻n=8, m=50,进行训练;
- 循环,直到找到最优参数。
Hyperband中每一次跑Successive Halving就在之前的Successive Halving结果上进行筛选。
pip install optunaimport optuna from sklearn import datasets from sklearn.model_selection import cross_val_score from sklearn.svm import SVC from sklearn.model_selection import train_test_split # 加载数据集 iris = datasets.load_iris() X = iris.data y = iris.target # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 定义目标函数 def objective(trial): C = trial.suggest_loguniform('C', 0.1, 10) gamma = trial.suggest_loguniform('gamma', 0.001, 0.1) kernel = trial.suggest_categorical('kernel', ['linear', 'rbf']) model = SVC(C=C, gamma=gamma, kernel=kernel) scores = cross_val_score(model, X_train, y_train, cv=5) return 1.0 - scores.mean() # 最大化准确率,即最小化1 - 准确率 # 创建 Optuna 研究 study = optuna.create_study(direction='minimize', sampler=optuna.samplers.TPESampler(), pruner=optuna.pruners.HyperbandPruner()) # 运行 Hyperband 优化 study.optimize(objective, n_trials=50) # 输出最佳参数 print("Best parameters found: ", study.best_params) # 使用最佳参数的模型进行预测 best_model = SVC(**study.best_params) best_model.fit(X_train, y_train) y_pred = best_model.predict(X_test) # 输出模型性能 from sklearn.metrics import accuracy_score print("Test accuracy: ", accuracy_score(y_test, y_pred))
网络架构搜索
NAS思路(与超参数优化相似)
- 搜索空间:网络超参数
- 搜索策略:
- 评估方法:
The One-shot Approach
- 只需要考虑架构与架构之间的评估排序,选出更好的架构,不需要要求数据集上精度
调参经验
- 记录调参数据
- 控制变量
- 代码版本控制
持续更新中,敬请期待!!!