机器学习基础知识
type
Post
status
Published
summary
机器学习是一门多学科交叉专业，本文主要是将学习机器学习的过程中可能会用到的一些基础知识进行整理，包括损失函数、正则项、矩阵和其他一些数学知识。
slug
machine-learning-base
date
May 1, 2020
tags
损失函数
正则化
优化函数
向量矩阵
category
机器学习
password
icon
URL
Property
Feb 28, 2024 01:10 PM
一、损失函数
损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好，通常模型的性能越好。不同的模型用的损失函数一般也不一样。训练集的平均损失称作经验风险损失，验风险损失加上正则项后，就是结构风险损失，此时的函数就是目标函数
常用的损失函数如下：
1.1、0-1损失
0-1损失是指预测值和目标值不相等为1， 否则为0:
0-1损失函数直接对应分类判断错误的个数，但是它是一个非凸函数，不太适用.
1.2、绝对值损失（L1损失）
绝对值损失函数是计算预测值与目标值的差的绝对值：
1.3、平方损失(L2损失)
也叫均方误差：
经常应用与回归问题
1.4、log对数损失
特点：
1、log对数损失函数能非常好的表征概率分布，在很多场景尤其是多分类，如果需要知道结果属于每个类别的置信度，那它非常适合。
2、健壮性不强，相比于hinge loss对噪声更敏感。
3、逻辑回归的损失函数就是log对数损失函数。
1.5、合页损失(hinge loss)
下标“+”表示取正值的函数，我们用z表示括号中的函数：
也就是说，数据点如果被正确分类，损失就为0，如果分类错误，损失为z，
SVM函数的损失函数就是hinge损失函数加上正则化项：
1.6、交叉熵损失
以二分类的栗子为例：
假设，当给定x，得到标签y=1的概率为：
那么，标签y=0的概率为：
公式可以整合为：
我们希望的是概率 P(y|x) 越大越好。首先，我们对 P(y|x) 引入 log 函数，因为 log 运算并不会影响函数本身的单调性。则有：
我们希望 越大越好，反过来，只要的负值越小就行了。
二、正则化项
以均方误差MSE为例，在我们用经验风险损失函数去求解模型的参数的过程中，我们会要求均方误差越小越好，但是一味的追求均方误差最小化，会导致模型出现过拟合现象：对训练样本预测效果很好，对测试样本的预测效果会很差。
解决过拟合现象的方法之一就是在我们的目标函数中加入正则化项~
- 这个正则化项是怎么来的呢？
- 为什么正则化项能够在一定程度上防止过拟合？
2.1、公式层面的理解
首先，我们的经验风险损失函数是：
我们要求这个损失函数的最小值，此时，系数w在对应的解空间内没有受到约束。要使模型不会过拟合，那模型就不能太复杂，要是模型不会太复杂，那么就要对系数w进行一定的约束。so
缩写s. t表示“Subject to”，是“服从某某条件”的意思，m表示样本的特征数，Z是约束常数。
此时，我们得到了一个不等式约束的最优化问题。并且以上不等式约束满足KKT条件，那么我们就可以构造一个拉格朗日函数：
公式中的z在求导之后就消除了，不影响的求解
2.2、图形层面的理解
假设一个样本X，特征维度是二，那么损失函数为
对系数w进行一定的约束
此时图形如下：
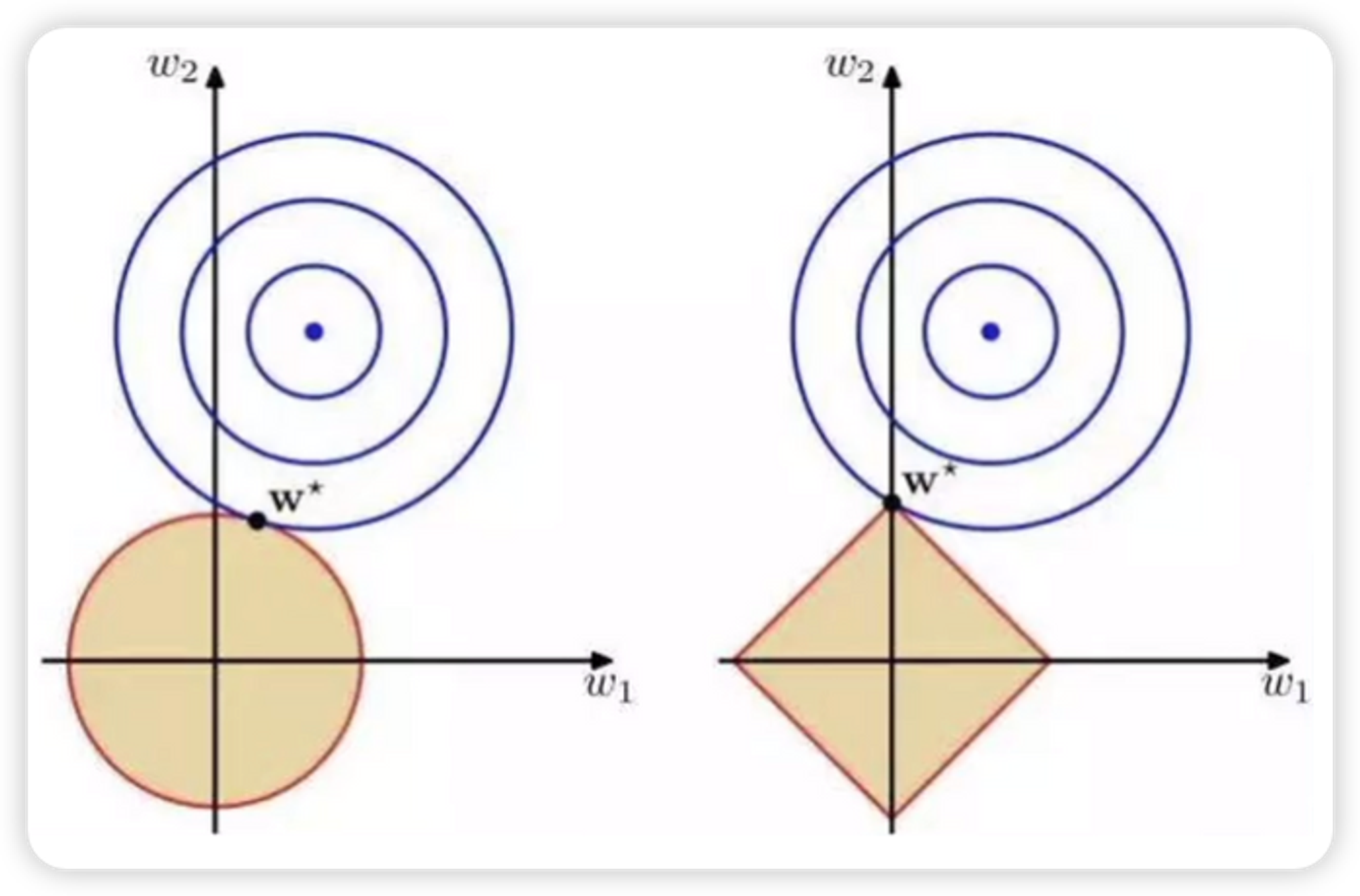
左图是L2正则，右图是L1正则。
- 解析：
- 此时w1和w2构成一个二维坐标的点
- 蓝色的点表示没有加正则项的损失函数的“最优”系数，蓝色的圆圈代表等值线，在同一个圆圈上的点算出来的均方误差是相同的。
- 暗黄色的图形表示我们规定的系数范围，系数w智能从这里面取值
- 整体的意思就是，在保证w落在暗黄色区域内的前提下，求出一个使得损失函数最小化的系数w 。也就是等值线和暗黄色区域相切的点，就是我们要找的最优点
- 在L1正则中，等值线与图形的顶点相交的可能性更大，这个时候w1=0，相当于系数就减少了；扩展到更高维也是同样的道理。
三、优化算法
优化算法的功能，是通过改善训练方式，来最小化(或最大化)损失函数E(x)。
在深度学习领域，优化算法的选择也是一个模型的重中之重。即使在数据集和模型架构完全相同的情况下，采用不同的优化算法，也很可能导致截然不同的训练效果。
3.1、梯度下降（Gradient Descent）
- 传统的批量梯度下降缺点
- 计算整个数据集梯度，但只会进行一次更新，因此在处理大型数据集时速度很慢且难以控制，甚至导致内存溢出。
- 在训练大型数据集时存在冗余的权重更新。
(1)、随机梯度下降（SGD）
待更新~
优化算法对比：
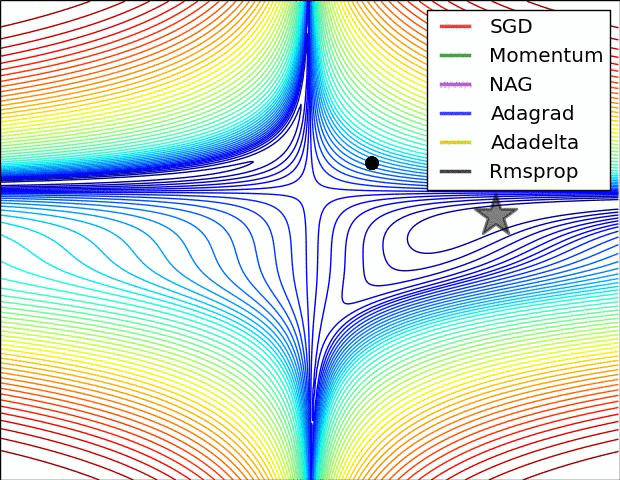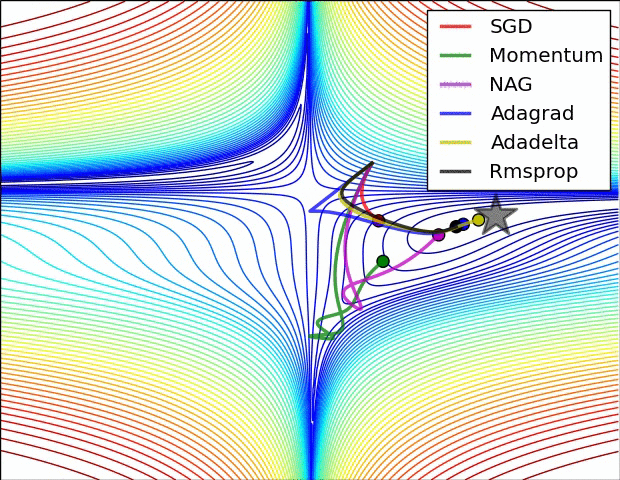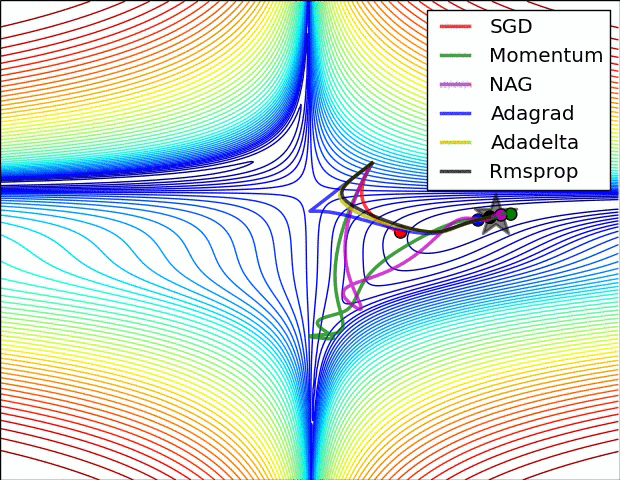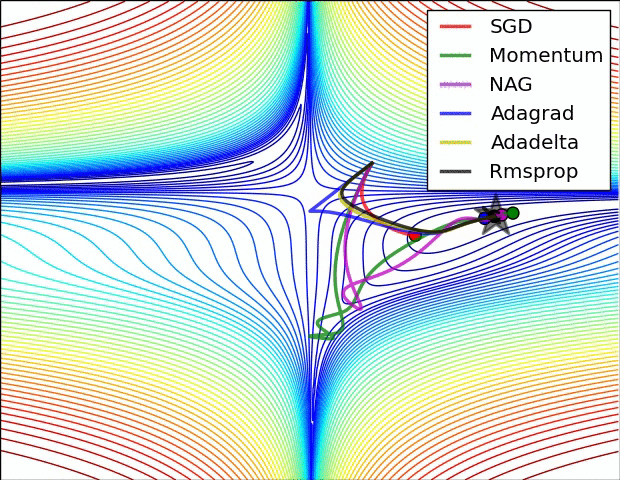
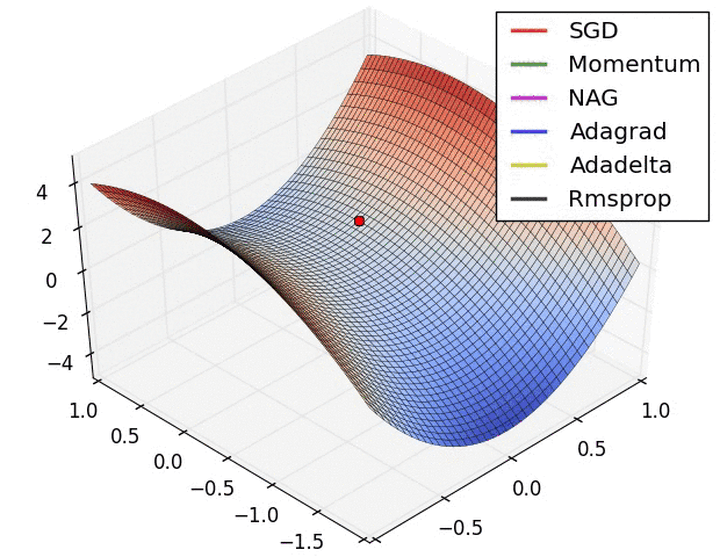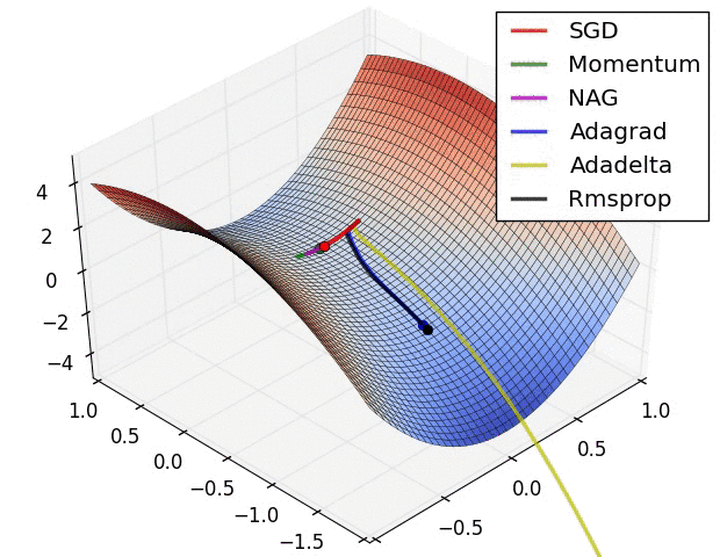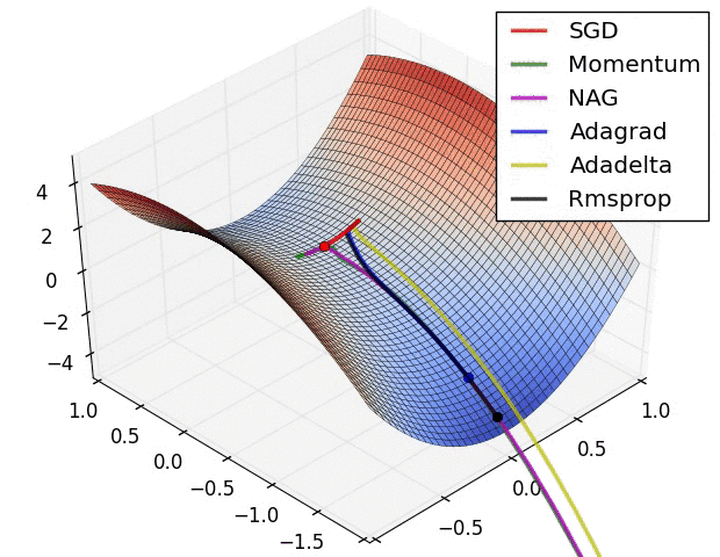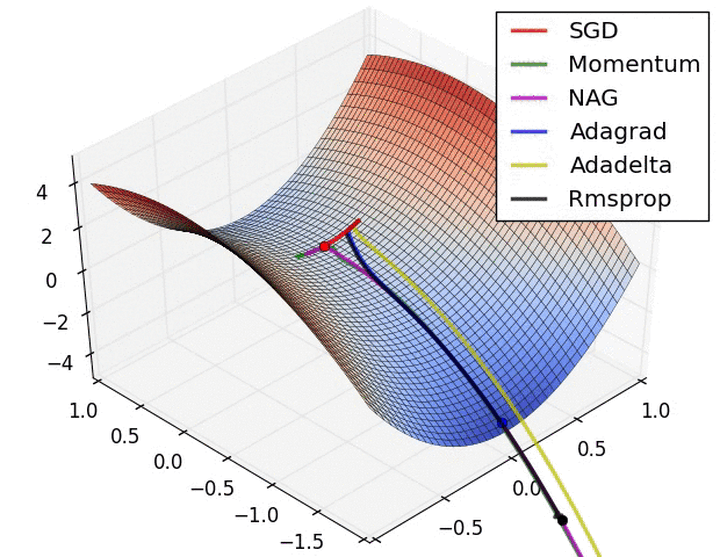
推荐阅读：
四、向量和矩阵
4.1、向量
向量是由n个实数组成的一个n行1列（n✖️1）或一个1行n列（1✖️n）的有序数组；
一个行向量乘以一个列向量称作向量的内积，又叫作点积，结果是一个数；
一个列向量乘以一个行向量称作向量的外积，外积是一种特殊的克罗内克积，结果是一个矩阵。
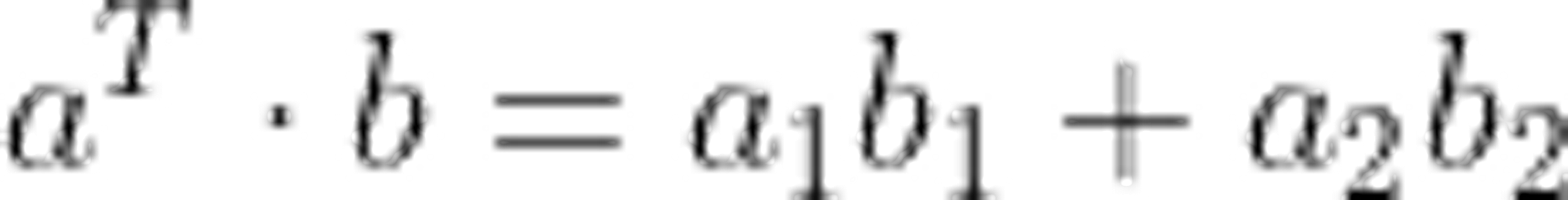
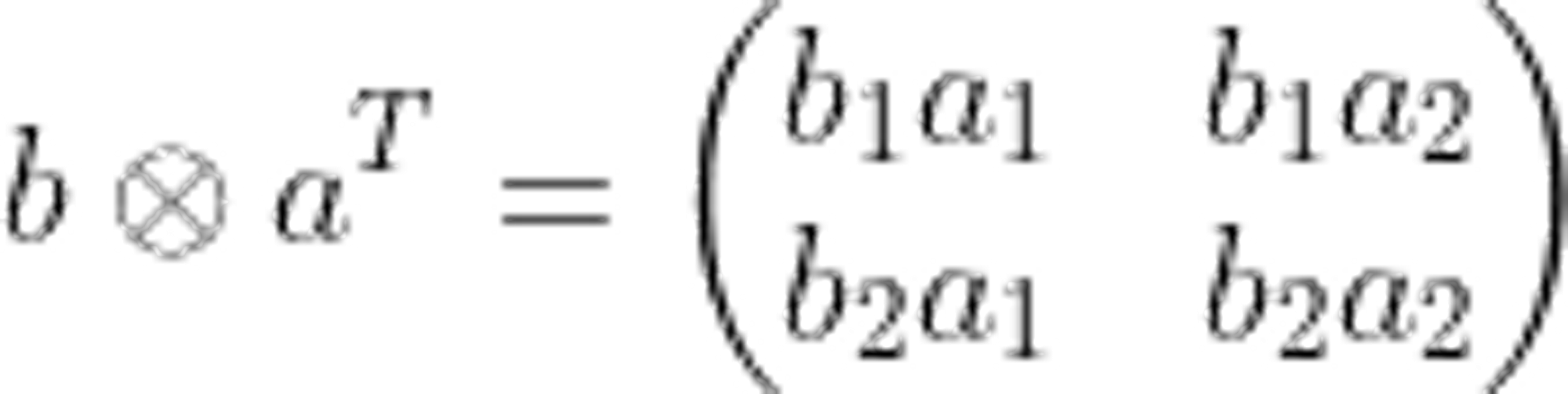
4.1.1、点乘
向量的点乘,也叫向量的内积、数量积，对两个向量执行点乘运算，就是对这两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。要求一维向量a和向量b的行列数相同。
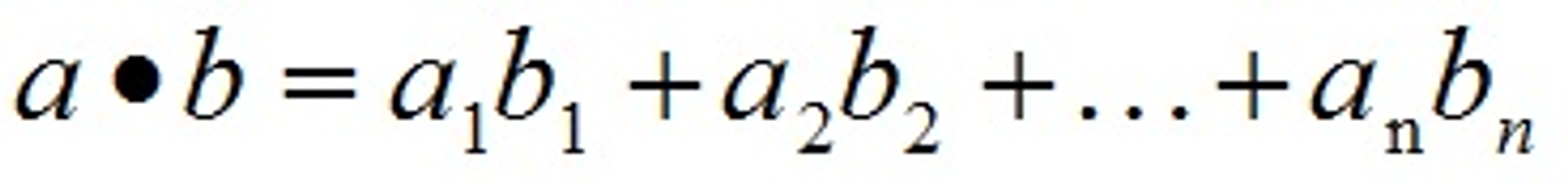
点乘几何意义：点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影
a·b>0 方向基本相同，夹角在0°到90°之间
a·b=0 正交，相互垂直
a·b<0 方向基本相反，夹角在90°到180°之间
4.1.2、叉乘
两个向量的叉乘，又叫向量积、外积、叉积，叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。
对于向量a和向量b：
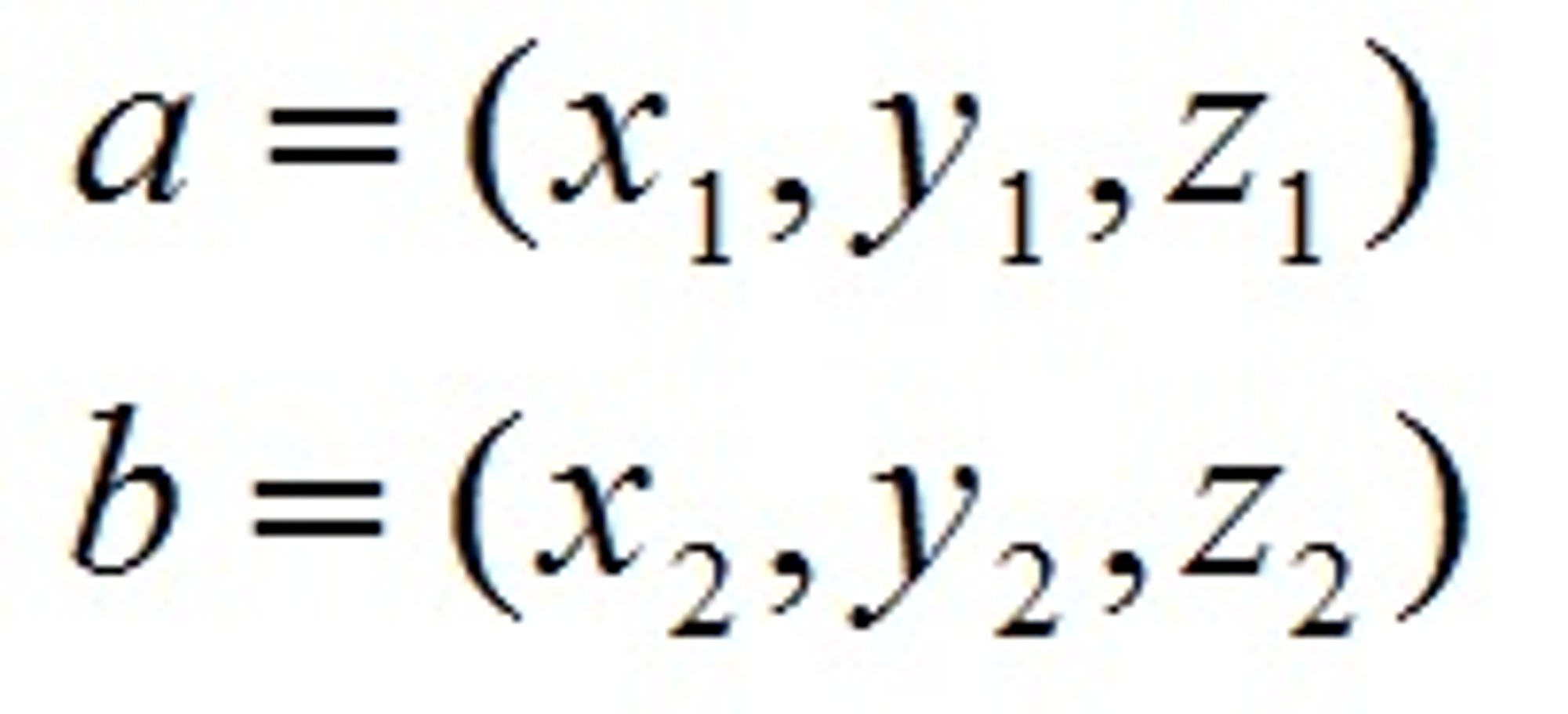
其中：
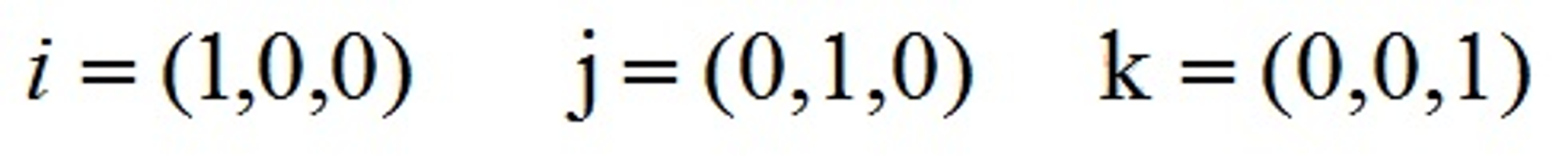
叉乘几何意义：在三维几何中，向量a和向量b的叉乘结果是一个向量，更为熟知的叫法是法向量，该向量垂直于a和b向量构成的平面。
4.2、矩阵
4.2.1、矩阵乘法
我觉得矩阵本身就可以看作是n维向量的有序集合，从这个角度来看，矩阵与矩阵的乘法就变成了矩阵与一堆向量的乘法，举个例子，可以这样看：C=AB这个矩阵乘法，如果把B这个矩阵看作是向量有序集合，那就是用矩阵A对B集合里面的列向量分别进行映射（或者说变换），得到的新矩阵C的列向量刚好等于B矩阵列向量分别经过A矩阵映射后得到的向量；如果把A看作是向量有序集合，右乘B矩阵就相当于用B矩阵对A矩阵中的各行向量进行映射（或者叫变换），得到的新矩阵C的行向量刚好等于A矩阵行向量分别经过B矩阵映射后得到的行向量，这个证明很直观，直接看矩阵乘法公式就一目了然了。最后得到的C每一列对应着右边那个矩阵B里的各列向量看，你会发现，正好是B里面那些列向量乘上A矩阵得到的结果；同理，右乘B也是一样的，只不过变成了行向量的映射罢了。
在numpy中对应的方法为np.dot()
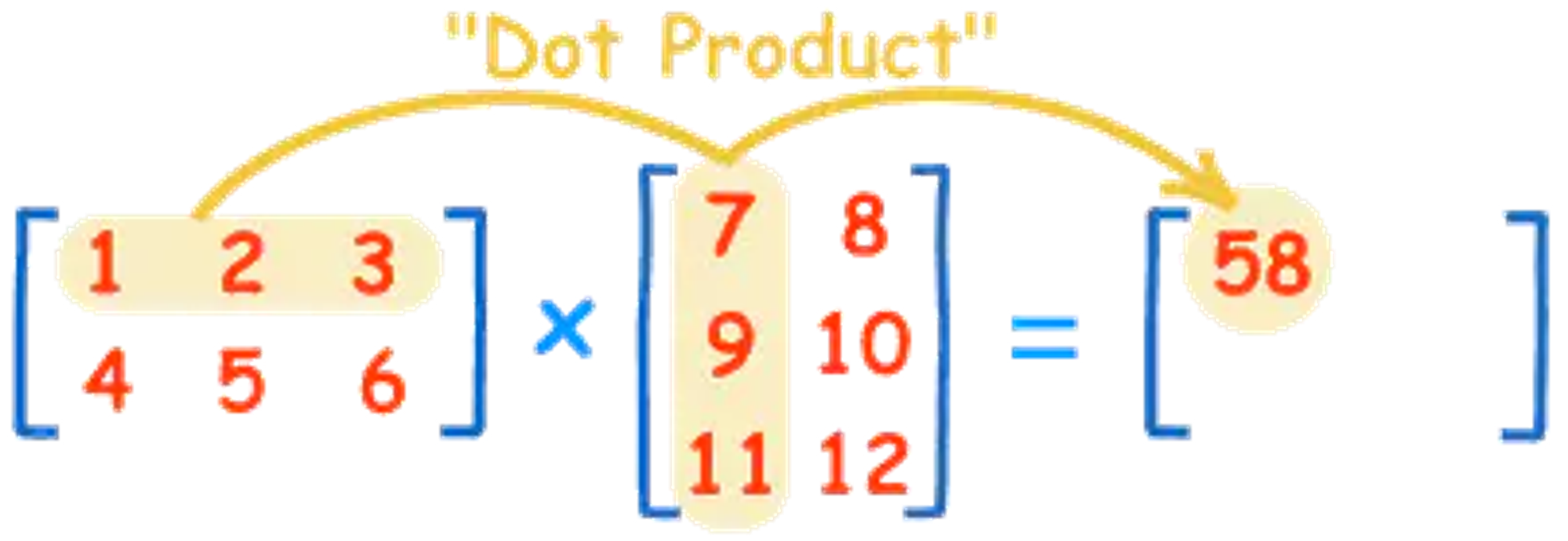
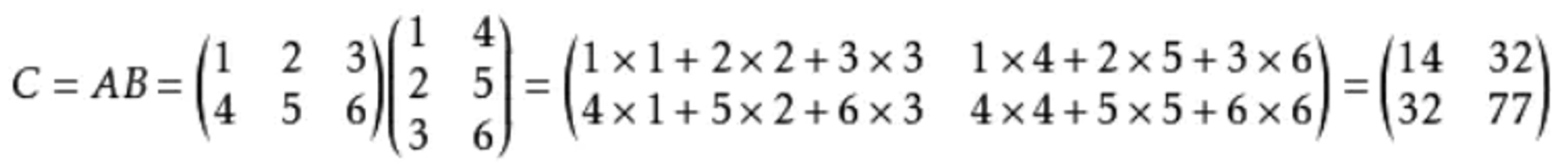
矩阵乘法证明
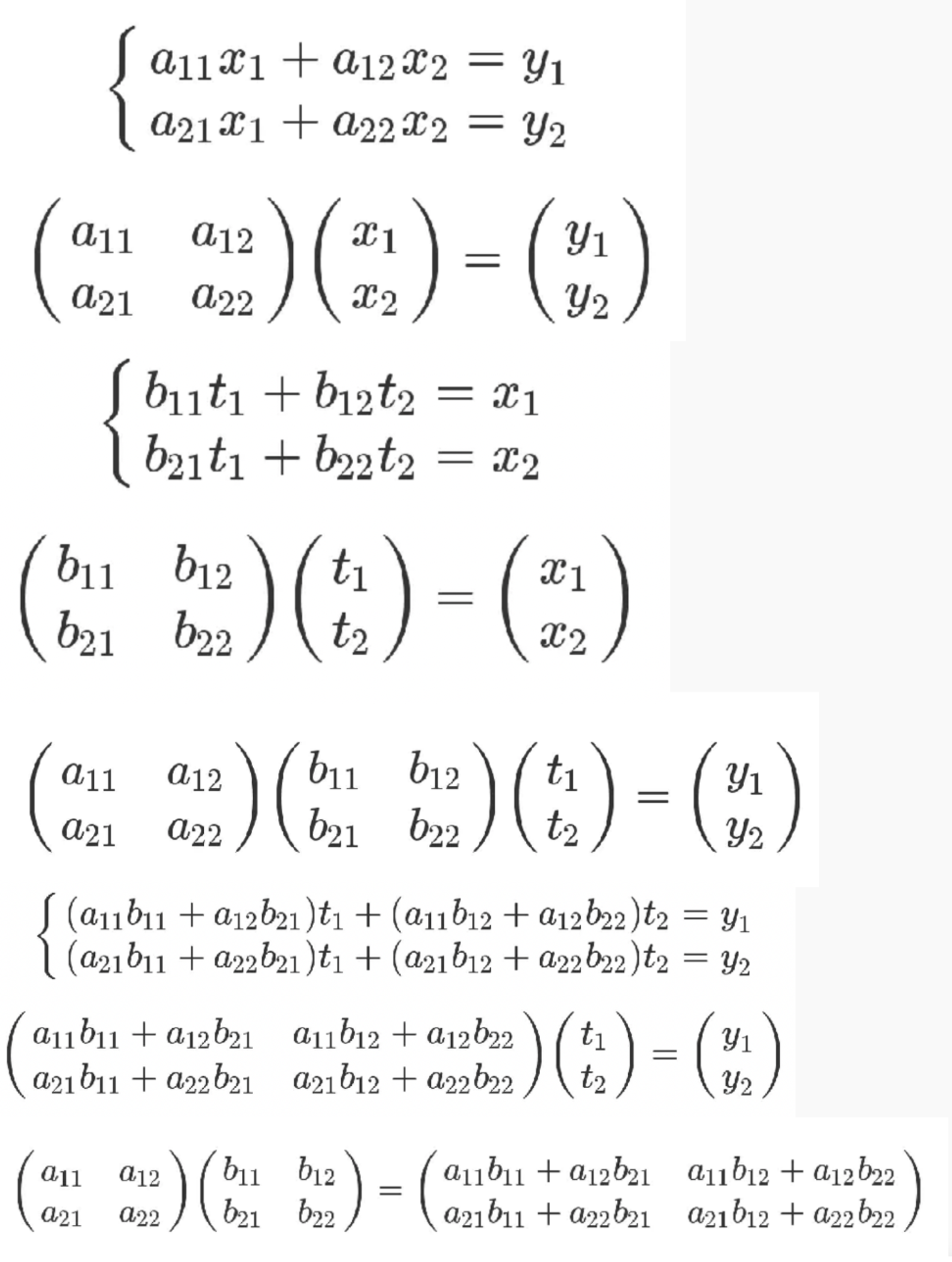
4.2.2、矩阵内积
两个相乘的矩阵维度一致，逐元素相乘，也叫哈达玛积(hadamard product)
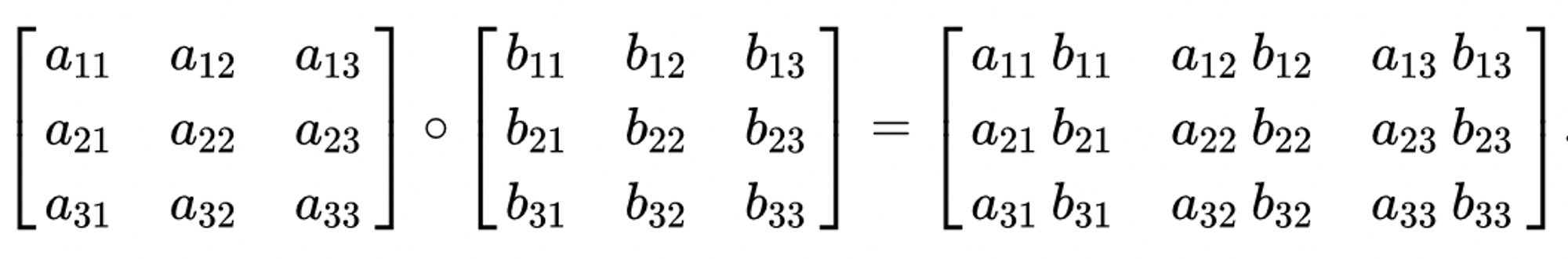
4.2.3、矩阵外积（叉乘）
外积是一种特殊的克罗内克积(Kronecker product)，克罗内克积是两个任意大小的矩阵间的运算，结果是一个矩阵
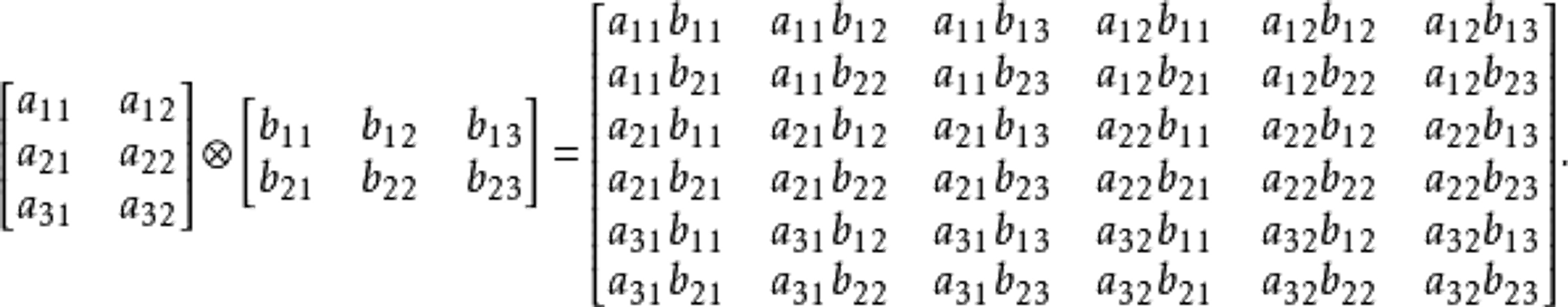
有争议，待验证：
如果想对一个矩阵进行行变换，可以左乘一个矩阵；相应的如果想对矩阵进行列变换，可以右乘一个矩阵。这种思想被应用到高斯消元的过程中。
4.3、矩阵分解
特征值
特征向量
特征分解
奇异矩阵分解
协方差矩阵
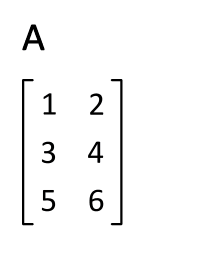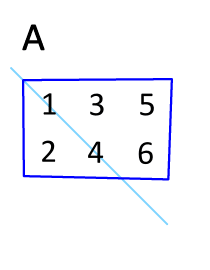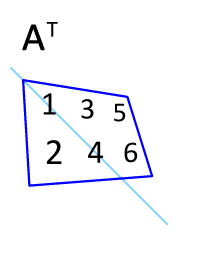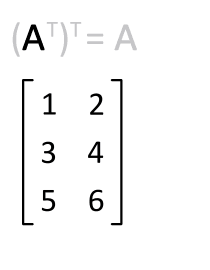
其他基础知识
1、最大似然估计
抛100次硬币，正面朝上的概率 抛100次硬币，第几次正面朝上的概率
公务员考试的考试次数与通过人数（共100人）
考试次数（X） | 1 | 2 | 3 | 4 | >4 |
通过人数 | 35 | 25 | 15 | 15 | 10 |
- 设：
- 考试次数为：X
- 通过考试的概率为：p
则考试三次通过的概率：
现在我们我们给出观测样本，要求概率p
(1)、方法一：大数定律
只看第一次考试，100人中，有35人通过；所以
大数定律只考虑了一部分人，会低估考试通过的概率
(2)、方法二：矩估计
根据公式 求概率p。【 表示样本的期望(平均值)，这里简单理解成每个人平均的考试次数(只算了次数小于四次的)】
据估计没有考虑到考试未通过的人群，会高估考试通过的概率
(3)、方法三：最大似然估计
极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！
对于离散型变量，最大似然函数等于概率：
则单独一个样本在第n次通过的概率：
求一个概率p使得 最大
解法①：求导，令倒数等于0，
解法②：两边同时取对数，在求导，令倒数等于0
最终 (最合理)
2、距离公式
对于距离的度量，我们有很多的距离度量方式：
欧式距离、L2距离：(Euclidean Distance)
曼哈顿距离、L1距离、城市街区距离：(Manhattan Distance)
切比雪夫距离：(Minkowski Distance)
闵可夫斯基距离:
闵氏距离不是一种距离， 而是一组距离的定义， 是对多个距离度量公式的概括性的表述。
当p=1时， 就是曼哈顿距离；
当p=2时， 就是欧氏距离；
当p→∞时， 就是切比雪夫距离。
推荐阅读：算法中各种距离的介绍