ARIMA及其衍生模型
type
Post
date
Jan 16, 2022
summary
ARIMA模型的基本思想是:将预测对象随时间推移而形成的数据序列视为一个随机序列,用一定的数学模型来近似描述这个序列,从而实现对未来值的预测。
category
学习笔记
tags
ARIMA
时序模型
预测模型
password
URL
Property
Jun 20, 2025 01:47 AM
一、相关模型
AR模型
- 自回归移动平均线 (Autoregressive Moving Average, ARMA)
- 自回归综合移动平均线 (Autoregressive Integrated Moving Average, ARIMA)
- 季节性自回归整合移动平均线 (Seasonal Autoregressive Integrated Moving-Average, SARIMA)
- 具有外生回归量的季节性自回归整合移动平均线 (Seasonal Autoregressive Integrated Moving-Average with Exogenous Regressors, SARIMAX)
VAR模型
- 向量自回归 (Vector Autoregression, VAR)
- 向量自回归移动平均 (Vector Autoregression Moving-Average, VARMA)
- 具有外源回归量的向量自回归移动平均值 (Vector Autoregression Moving-Average with Exogenous Regressors, VARMAX)
二、数据平稳
一般时序模型都要求数据是平稳的。
平稳:平稳分为严平稳和宽平稳,严平稳保证时间序列的任何有限维分布对于时间的平移是不变的;宽平稳则要求协方差结构随时间的平移而不变,又称为二阶矩平稳序列。平稳的意义是使得时间序列的根本特征不随着时间的变化而发生改变。
2.1、判断数据是否平稳
除了用肉眼判断的方法,另外比较常用的严格的统计检验方法就是ADF检验,也叫做单位根检验。
ADF检验可以通过python中的 statsmodels 模块的adfuller函数实现
adfuller函数参数及返回值详解:
# adfuller函数参数 x: array_like,1d,要测试的数据系列。 maxlag: 测试中包含的最大延迟,默认为12 *(nobs / 100)^ {1/4}。 regression: {‘c’,‘ct’,‘ctt’,‘nc’}, 包含在回归中的常量和趋势顺序。‘c’:仅限常量(默认值)。 ‘ct’:恒定和趋势。 ‘ctt’:常数,线性和二次趋势。 ‘nc’:没有恒定,没有趋势。 autolag: {‘AIC’,‘BIC’,‘t-stat’,None}自动确定滞后时使用的方法。如果为None,则使用maxlag滞后。如果是’AIC’(默认值)或’BIC’,则选择滞后数以最小化相应的信息标准。基于’t-stat’的maxlag选择。从maxlag开始并使用5%大小的测试来降低延迟,直到最后一个滞后长度的t统计量显着为止。 store: bool,如果为True,则另外返回adf统计信息的结果实例。默认值为False。 regresults: bool,optional,如果为True,则返回完整的回归结果。默认值为False。 # adfuller函数返回值 ADF:float, 测试统计。 pvalue:float, probability value:MacKinnon基于MacKinnon的近似p值(1994年,2010年)。 usedlag:int, 使用的滞后数量。 NOBS:int, 用于ADF回归和计算临界值的观察数。 critical values:dict, 测试统计数据的临界值为1%,5%和10%。基于MacKinnon(2010)。 icbest:float, 如果autolag不是None,则最大化信息标准。 resstore:ResultStore, optional, 一个虚拟类,其结果作为属性附加。
简单实现:
from statsmodels.tsa.stattools import adfuller timeseries = data # 被检验数据 adftest = adfuller(timeseries,autolag = 'AIC') # ADF检验 # 返回值实例 (-1.6596695973336932, 0.9169218489129718, 0, 230, {'1%': -4.422218041176954, '5%': -3.8583127840881075, '10%': -3.569276584942878}, 1640.0264270221523)可以看到,依次为ADF, p-value, usedlag, nobs, critical-value, AIC这几个参数。
如何根据结果怕断数据是否平稳
若ADF值同时小于critical-value中1%,5%,10%对应的值,则说明数据平稳。
对上面的实例进行分析
(-1.6596695973336932, 0.9169218489129718, 0, 230, {'1%': -4.422218041176954, '5%': -3.8583127840881075, '10%': -3.569276584942878}, 1640.0264270221523) # -1.66比返回值的critical-value中的三个值都要大,说明数据不平稳
2.2、使用差分平稳数据
对不平稳的数据,我们可以进行差分,使其平稳
# 对数据差分 diff1 = timeseries.diff(1).dropna() # 1阶差分 # 再进行平稳性判断 adftest_diff1 = adfuller(diff1,autolag = 'AIC') ## 若1阶差分不能使数据平稳,则继续2阶差分,以此类推(也可以在一阶差分的基础上再进行一阶差分) diff2 = timeseries.diff(2).dropna() # 1阶差分 # 再进行平稳性判断 adftest_diff2 = adfuller(diff2,autolag = 'AIC')
2.3、案例实现
# 数据平稳性检测 因为只有平稳数据才能做时间序列分析 import statsmodels.tsa.stattools as ts def judge_stationarity(data_sanya_one): dftest = ts.adfuller(data_sanya_one) stationarity = 1 for key, value in dftest[4].items(): if dftest[0] > value: stationarity = 0 print("是否平稳(1/0): %d" %(stationarity)) return stationarity stationarity = judge_stationarity(all_data_list)
三、SARIMAX模型
3.1、模型参数
from statsmodels.tsa.statespace.sarimax import SARIMAX statsmodels.tsa.statespace.sarimax.SARIMAX(endog, exog=None, order=(1, 0, 0), seasonal_order=(0, 0, 0, 0), trend=None) # 以上只列出了主要参数, # endog:训练数据 # exog:外部变量 # order:自回归,差分,滑动平均项 (p,d,q) # seasonal_order:季节因素的自回归,差分,移动平均,周期 (P,D,Q,s) # trend:趋势,c表示常数,t:线性,ct:常数+线性
如果不指定seasonal_order或者季节性参数都设定为0,那么就是普通的ARIMA模型,exog外部因子没有也可以不用指定
其他的参数如无必要,则不需要修改,因为函数默认的参数在大多数时候是最优的;
3.2、模型评估方法
总的来说,SARIMA 模型通过(p,d,q) (P,D,Q,m)不同的组合,囊括了ARIMA, ARMA, AR, MA模型,使用指定的模型评估准则,选择最优模型
模型评估准则:
1、AIC信息准则:常常使用AIC和BIC作为模型优劣的衡量标准,该标准只能说在这么多备选模型中,最小AIC的模型刻画的真实数据表达的信息损失最小,是相对指标。
AIC在样本容量很大时,拟合所得数值会因为样本容量而放大(通常超过1000的样本称之为大样本容量)。AIC和BIC作为模型选择的准则,可以有效弥补根据自相关图和偏自相关图定阶的主观性。
2、各种评价指标:最常用的是MAPE(平均绝对误差百分比)
MAPE也是反映误差大小的相对值,不同模型对同一数据的模型进行评估才有比较的意义。
3、Box-Jenkins检验准则:Box-Jenkins 建模流程如下,建立在反复验证是否满足假设前提,并对参数调整。
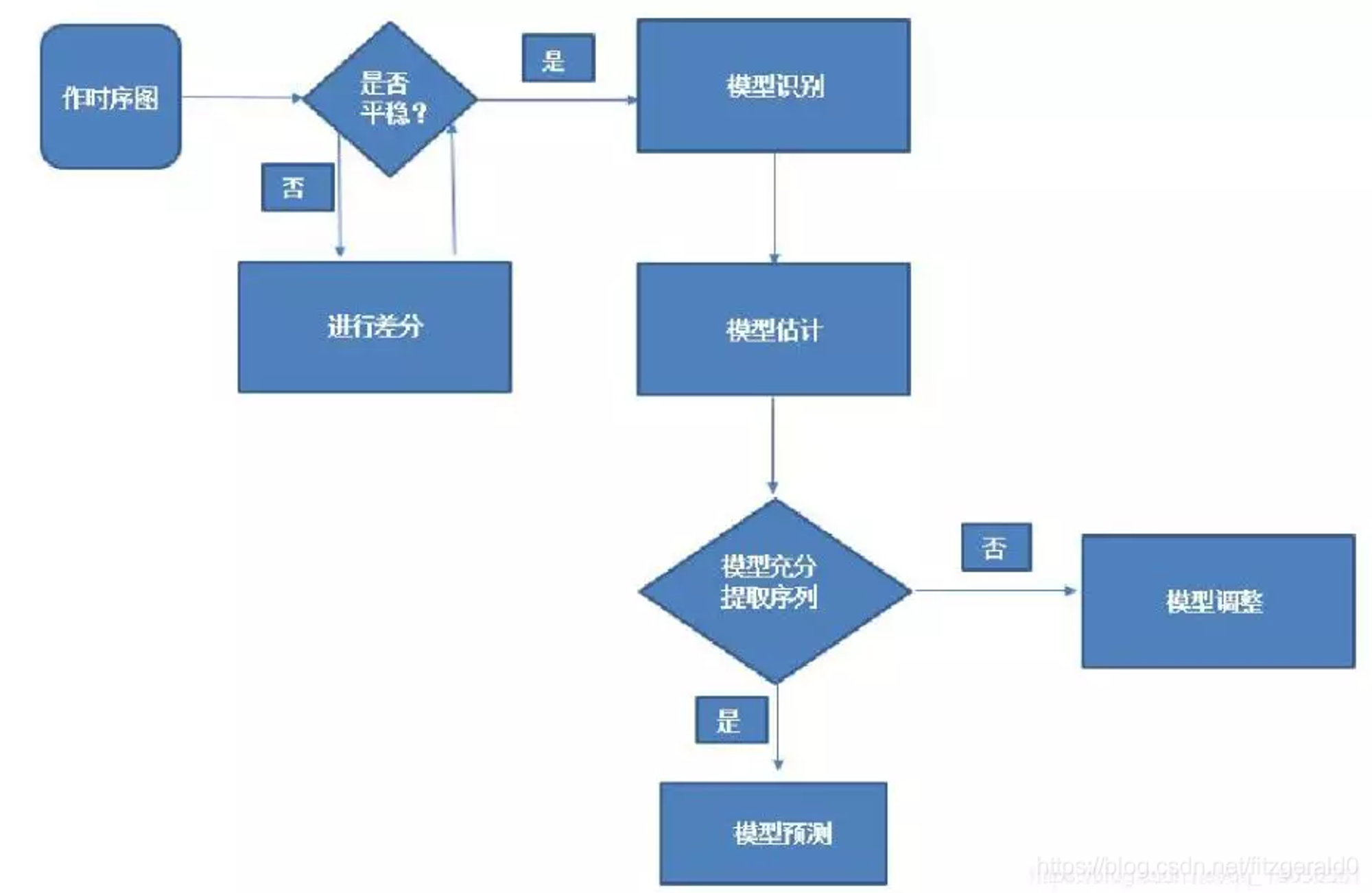
三种建模评估标准,最好综合考虑,AIC从信息论的角度度量信息损失大小, Box-Jenkins是传统的层层假设之下的时间序列统计建模准则,在应对单一序列模型,通过眼观图形和检验参数的显著性来判定,效果佳。而如果我们关注的是模型准确率,那么最好的当然是MAPE等关注预测准确性的指标,此时不能无脑的用函数原始的定义或者AIC
3.3、模型参数确定
3.3.1、参数order(p、d、q)
1、时间序列的差分:d
如果对时间序列做 d 次差分才能得到一个平稳序列,那么这个次数就是order(p、d、q)中的d
2、自回归:p,滑动平均项:q
观图查找
通过自相关(ACF)和偏自相关(PACF)图找到p、q值;推荐阅读:如何根据自相关(ACF)图和偏自相关(PACF)图选择ARIMA模型的p、q值
ACF和PACF图的含义和特性
含义
Autocorrelation Function (ACF)自相关函数,指任意时间 t(t=1,2,3…n)的 序列值Xt 与其自身的滞后(这里取滞后一阶,即lag=1)值Xt-1之间的线性关系;ACF图就是指以滞后值(上图就是滞后值为 1阶)为x轴,自相关系数(Xt与Xt-1的相关系数值)为y轴画出的图,也叫做相关图。PACF图就是部分相关图。
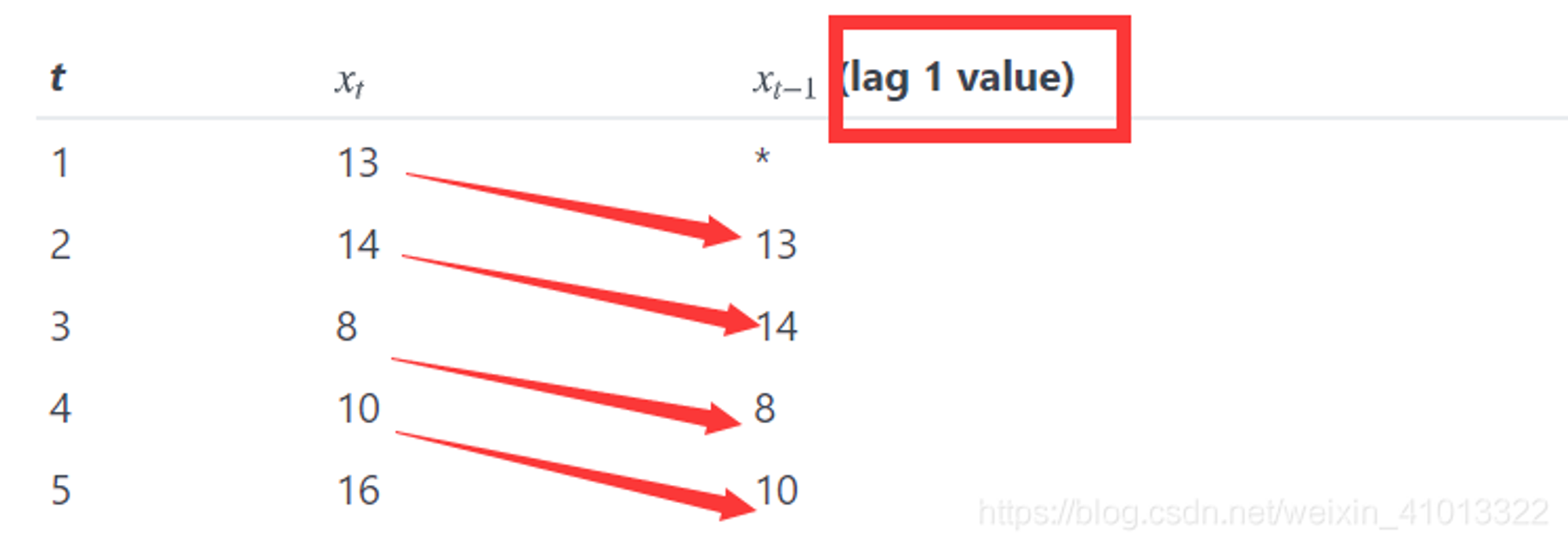
特性
截尾:在大于某个常数k后快速趋于0为k阶截尾
拖尾:始终有非零取值,不会在k大于某个常数后就恒等于零(或在0附近随机波动)
ㅤ | AR ( p) | MA(q) | ARMA(p,q) |
ACF | 拖尾 | q阶后截断 | 拖尾q |
PACF | p阶后截断 | 拖尾 | 拖尾p |
ACF和PACF图案例分析
ACF拖尾,PACF截尾
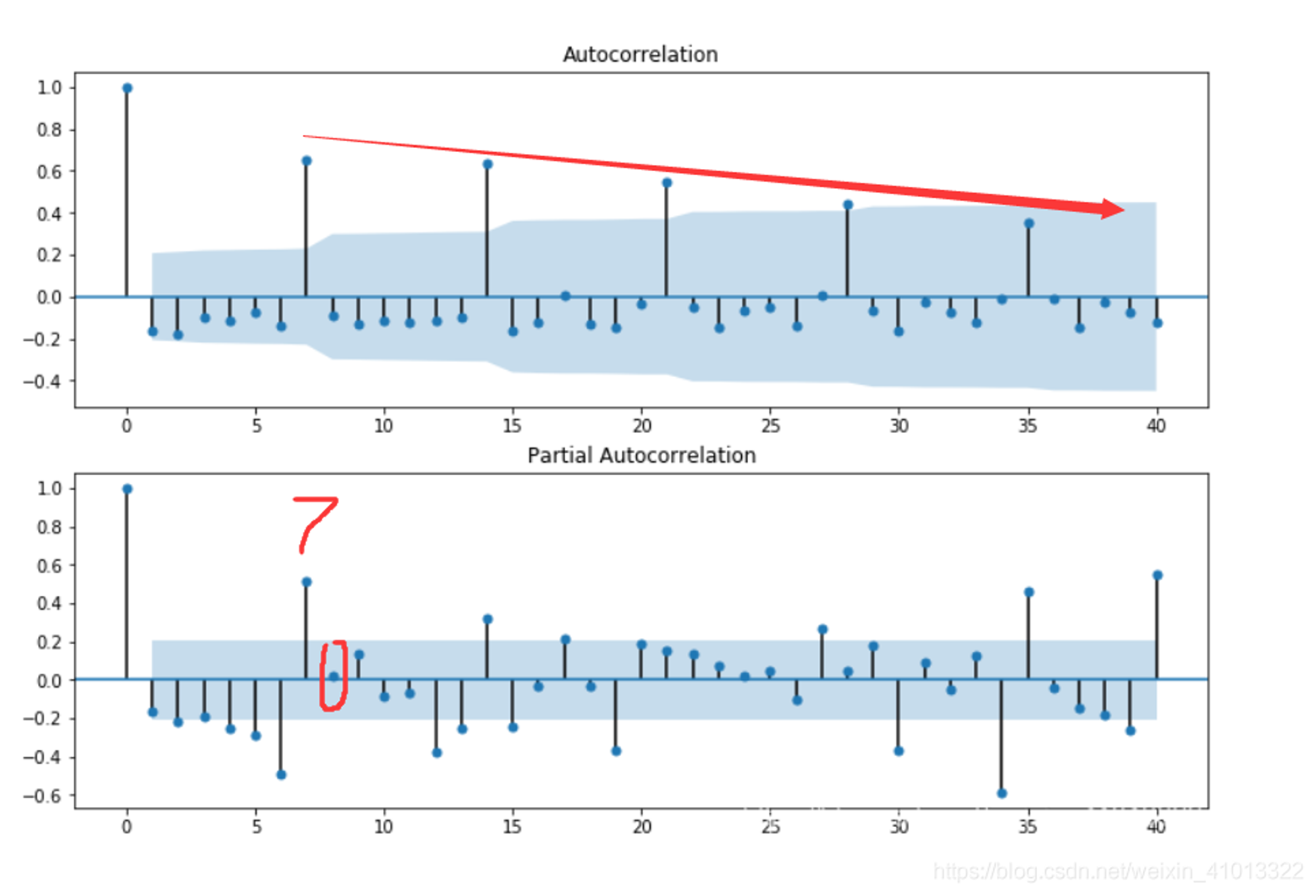
第一个图为ACF,第二个图为PACF。
可以看到ACF是一个逐渐趋于0的拖尾,而PACF在7阶过后系数为0,所以模型是AR(7)或AR(8),即ARMA(7,0)或ARMA(8,0)。备选模型ARMA(7,1)。
ACF和PACF都拖尾
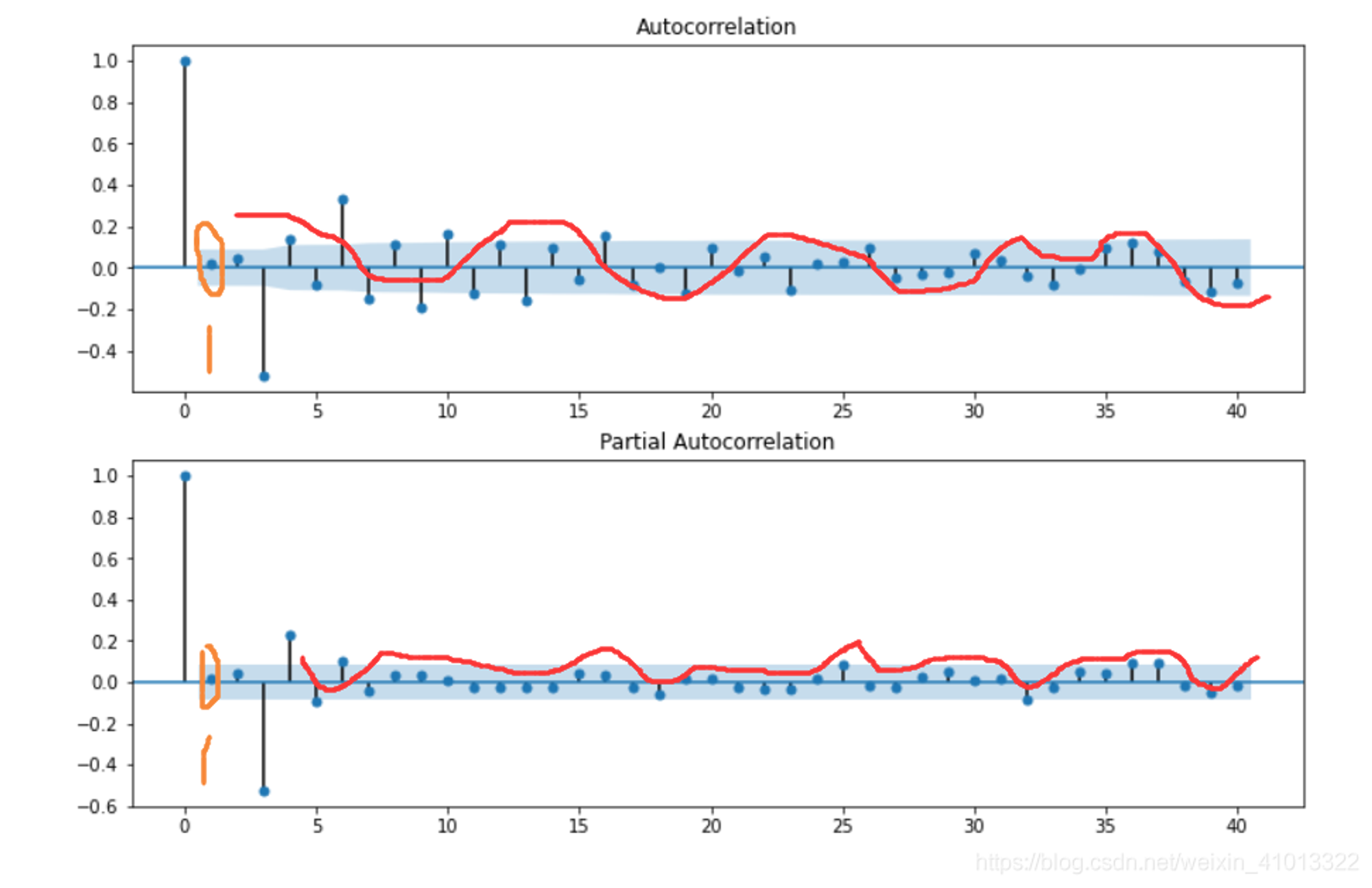
ACF和PACF都呈现拖尾,在1阶位置就开始基本落在2倍标准差范围,所以是ARMA(1,1)模型。
找到合适数值的多组参数之后,可以通过模型的AIC(赤池信息量),BIC(贝叶斯信息量),HQIC等值确定哪一组最好,AIC,BIC数值越小,参数越合适。
自动查找
选定模型后,根据各组参数对应的AIC值来选择数值最小的一组参数;可以手动实现,也可以调用函数实现。
手动实现
from statsmodels.tsa.arima_model import ARIMA pmax = int(5) #一般阶数不超过 length /10 qmax = int(5) bic_matrix = [] for p in range(pmax +1): temp= [] for q in range(qmax+1): try: temp.append(ARIMA(all_data_list, (p, 0, q)).fit().bic) except: temp.append(None) bic_matrix.append(temp) bic_matrix1 = pd.DataFrame(bic_matrix) # 将其转换成Dataframe 数据结构 p,q = bic_matrix1.stack().idxmin() # 先使用stack 展平, 然后使用 idxmin 找出最小值的位置 print(u'BIC 最小的p值 和 q 值:%s,%s' %(p,q)) # BIC 最小的p值 和 q 值:6,1
函数实现


3.3.2、参数seasonal_order(P,D,Q,s) 和参数 trend
使用网格搜索对这两个参数进行确定,一般P,D,Q通常为(0,1,2)中的数值,s为数据周期